思考并回答以下问题:
上节课我讲到了索引的作用,是否需要建立索引,以及建立什么样的索引,需要我们根据实际情况进行选择。我之前说过,索引其实就是一种数据结构,那么今天我们就来看下,索引的数据结构究竟是怎样的?对索引底层的数据结构有了更深入的了解后,就会更了解索引的使用原则。
今天的文章内容主要包括下面几个部分:
1,为什么索引要存放到硬盘上?如何评价索引的数据结构设计的好坏?
2,使用平衡二叉树作为索引的数据结构有哪些不足?
3,B树和B+树的结构是怎样的?为什么我们常用B+树作为索引的数据结构?
如何评价索引的数据结构设计好坏
数据库服务器有两种存储介质,分别为硬盘和内存。内存属于临时存储,容量有限,而且当发生意外时(比如断电或者发生故障重启)会造成数据丢失;硬盘相当于永久存储介质,这也是为什么我们需要把数据保存到硬盘上。
虽然内存的读取速度很快,但我们还是需要将索引存放到硬盘上,这样的话,当我们在硬盘上进行查询时,也就产生了硬盘的I/O操作。相比于内存的存取来说,硬盘的I/O存取消耗的时间要高很多。我们通过索引来查找某行数据的时候,需要计算产生的磁盘I/O次数,当磁盘I/O次数越多,所消耗的时间也就越大。如果我们能让索引的数据结构尽量减少硬盘的I/O操作,所消耗的时间也就越小。
二叉树的局限性
二分查找法是一种高效的数据检索方式,时间复杂度为O(log2n),是不是采用二叉树就适合作为索引的数据结构呢?
我们先来看下最基础的二叉搜索树(Binary Search Tree),搜索某个节点和插入节点的规则一样,我们假设搜索插入的数值为key:
1,如果key大于根节点,则在右子树中进行查找;
2,如果key小于根节点,则在左子树中进行查找;
3,如果key等于根节点,也就是找到了这个节点,返回根节点即可。
举个例子,我们对数列(34,22,89,5,23,77,91)创造出来的二分查找树如下图所示:
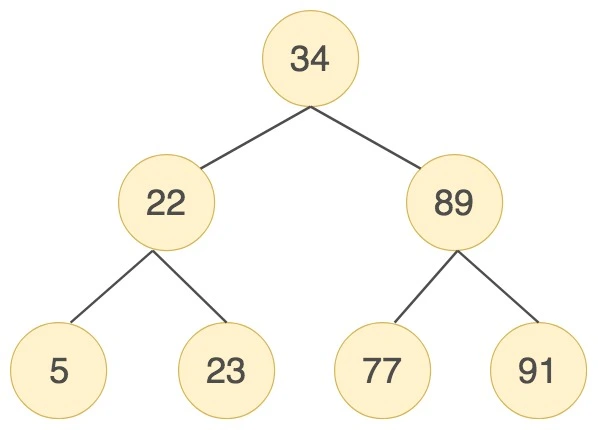
但是存在特殊的情况,就是有时候二叉树的深度非常大。比如我们给出的数据顺序是(5,22,23,34,77,89,91),创造出来的二分搜索树如下图所示:

你能看出来第一个树的深度是3,也就是说最多只需3次比较,就可以找到节点,而第二个树的深度是7,最多需要7次比较才能找到节点。
第二棵树也属于二分查找树,但是性能上已经退化成了一条链表,查找数据的时间复杂度变成了O(n)。为了解决这个问题,人们提出了平衡二叉搜索树(AVL树),它在二分搜索树的基础上增加了约束,每个节点的左子树和右子树的高度差不能超过1,也就是说节点的左子树和右子树仍然为平衡二叉树。
这里说一下,常见的平衡二叉树有很多种,包括了平衡二叉搜索树、红黑树、数堆、伸展树。平衡二叉搜索树是最早提出来的自平衡二叉搜索树,当我们提到平衡二叉树时一般指的就是平衡二叉搜索树。事实上,第一棵树就属于平衡二叉搜索树,搜索时间复杂度就是O(log2n)。
我刚才提到过,数据查询的时间主要依赖于磁盘I/O的次数,如果我们采用二叉树的形式,即使通过平衡二叉搜索树进行了改进,树的深度也是O(log2n),当n比较大时,深度也是比较高的,比如下图的情况:
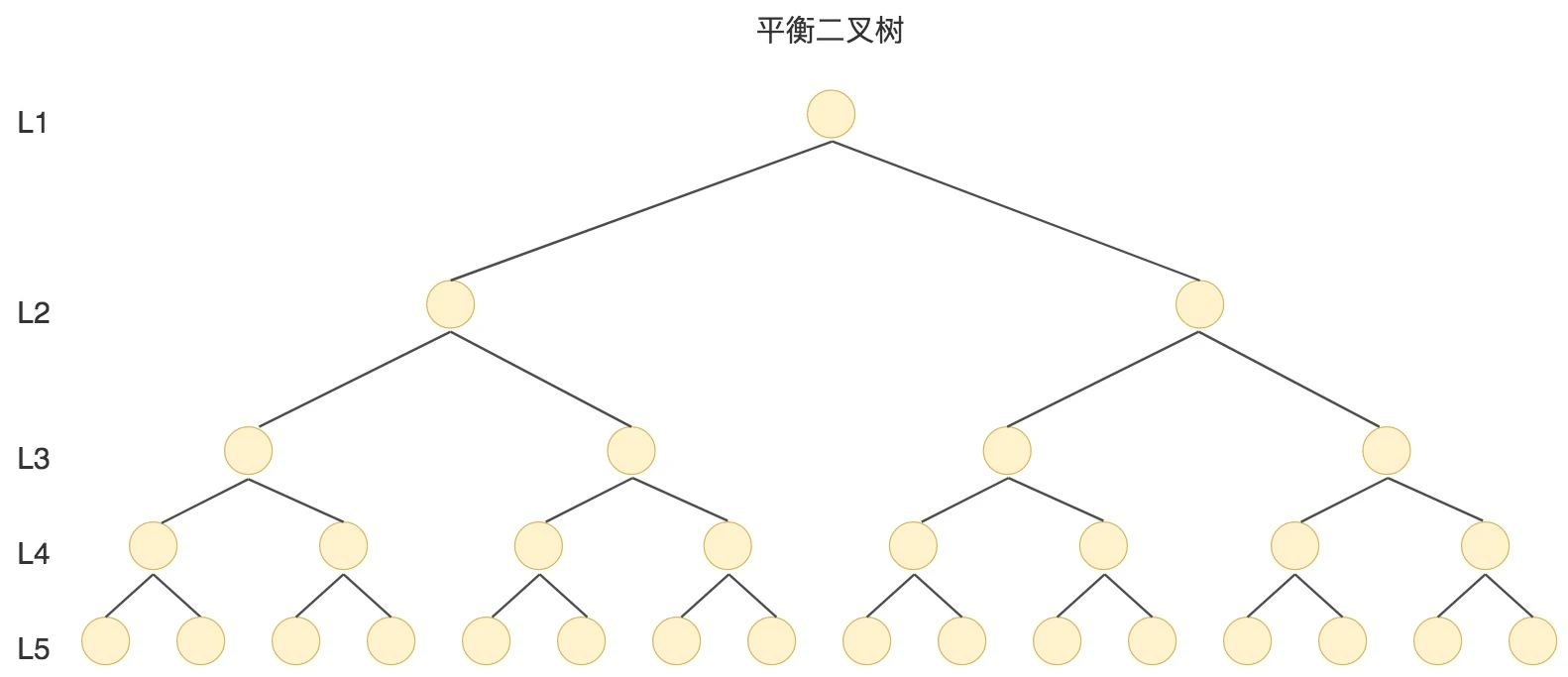
每访问一次节点就需要进行一次磁盘I/O操作,对于上面的树来说,我们需要进行5次I/O操作。虽然平衡二叉树比较的效率高,但是树的深度也同样高,这就意味着磁盘I/O操作次数多,会影响整体数据查询的效率。
针对同样的数据,如果我们把二叉树改成M叉树(M>2)呢?当M=3时,同样的31个节点可以由下面的三叉树来进行存储:
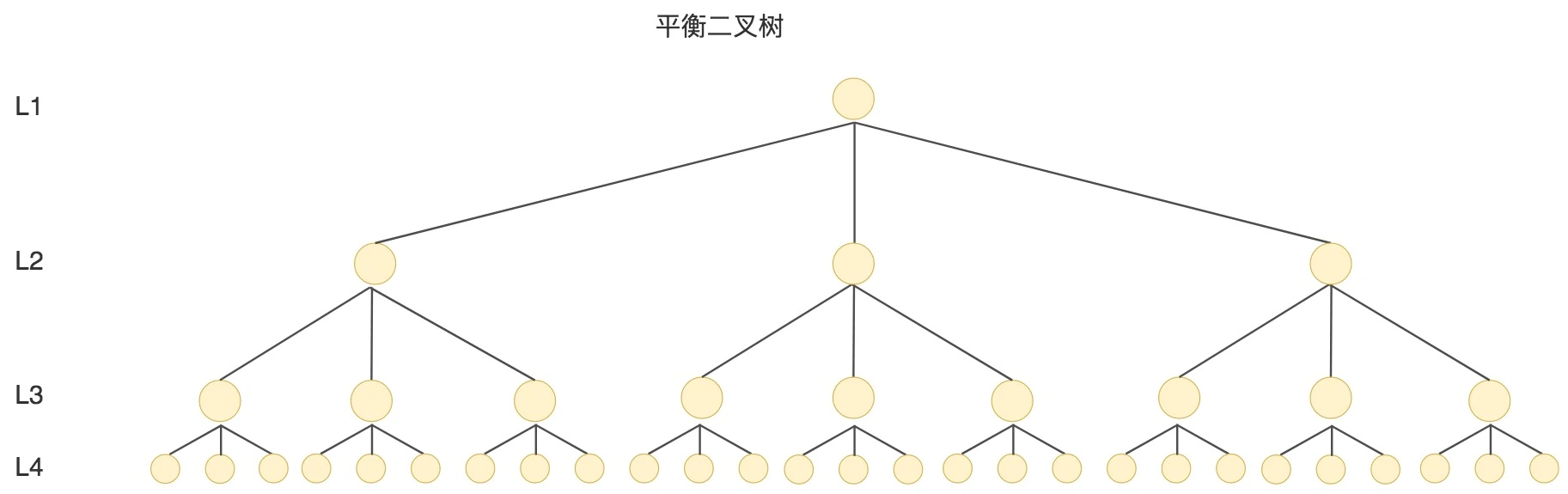
你能看到此时树的高度降低了,当数据量N大的时候,以及树的分叉数M大的时候,M叉树的高度会远小于二叉树的高度。
什么是B树
如果用二叉树作为索引的实现结构,会让树变得很高,增加硬盘的I/O次数,影响数据查询的时间。因此一个节点就不能只有2个子节点,而应该允许有M个子节点(M>2)。
B树的出现就是为了解决这个问题,B树的英文是BalanceTree,也就是平衡的多路搜索树,它的高度远小于平衡二叉树的高度。在文件系统和数据库系统中的索引结构经常采用B树来实现。
B树的结构如下图所示:
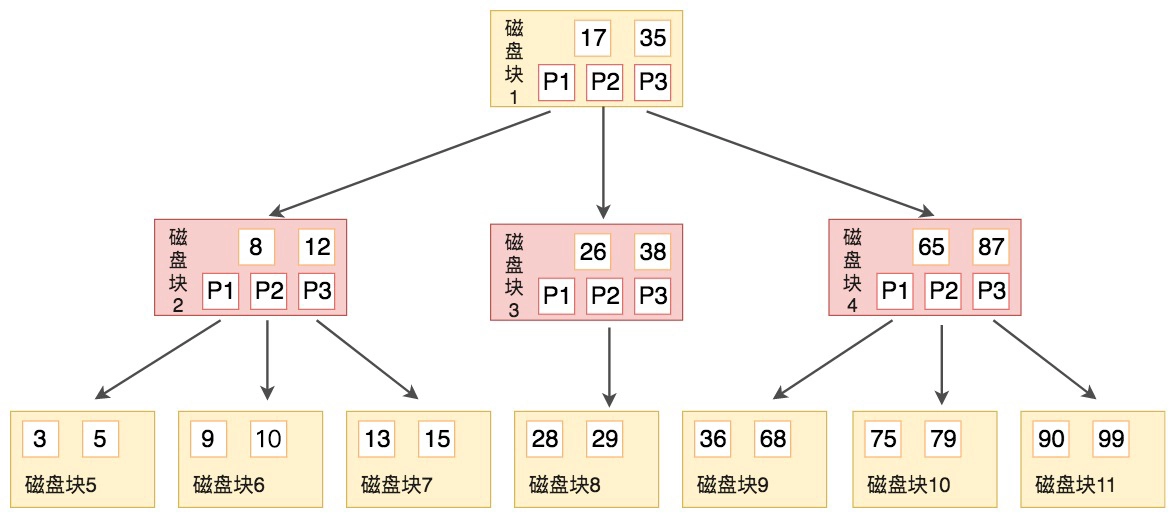
B树作为平衡的多路搜索树,它的每一个节点最多可以包括M个子节点,M称为B树的阶。同时你能看到,每个磁盘块中包括了关键字和子节点的指针。如果一个磁盘块中包括了x个关键字,那么指针数就是x+1。对于一个100阶的B树来说,如果有3层的话最多可以存储约100万的索引数据。对于大量的索引数据来说,采用B树的结构是非常适合的,因为树的高度要远小于二叉树的高度。
一个M阶的B树(M>2)有以下的特性:
1,根节点的儿子数的范围是[2,M]。
2,每个中间节点包含k-1个关键字和k个孩子,孩子的数量=关键字的数量+1,k的取值范围为[ceil(M/2),M]。
3,叶子节点包括k-1个关键字(叶子节点没有孩子),k的取值范围为[ceil(M/2),M]。
4,假设中间节点节点的关键字为:Key[1],Key[2],…,Key[k-1],且关键字按照升序排序,即Key[i]<Key[i+1],此时k-1个关键字相当于划分了k个范围,也就是对应着k个指针,即为:P[1],P[2],…,P[k],其中P[1]指向关键字小于Key[1]的子树,P[i]指向关键字属于(Key[i-1],Key[i])的子树,P[k]指向关键字大于Key[k-1]的子树。
5,所有叶子节点位于同一层。
上面那张图所表示的B树就是一棵3阶的B树。我们可以看下磁盘块2,里面的关键字为(8,12),它有3个孩子(3,5),(9,10)和(13,15),你能看到(3,5)小于8,(9,10)在8和12之间,而(13,15)大于12,刚好符合刚才我们给出的特征。
然后我们来看下如何用B树进行查找。假设我们想要查找的关键字是9,那么步骤可以分为以下几步:
1,我们与根节点的关键字(17,35)进行比较,9小于17那么得到指针P1;
2,按照指针P1找到磁盘块2,关键字为(8,12),因为9在8和12之间,所以我们得到指针P2;
3,按照指针P2找到磁盘块6,关键字为(9,10),然后我们找到了关键字9。
你能看出来在B树的搜索过程中,我们比较的次数并不少,但如果把数据读取出来然后在内存中进行比较,这个时间就是可以忽略不计的。而读取磁盘块本身需要进行I/O操作,消耗的时间比在内存中进行比较所需要的时间要多,是数据查找用时的重要因素,B树相比于平衡二叉树来说磁盘I/O操作要少,在数据查询中比平衡二叉树效率要高。
什么是B+树
B+树基于B树做出了改进,主流的DBMS都支持B+树的索引方式,比如MySQL。B+树和B树的差异在于以下几点:
1,有k个孩子的节点就有k个关键字。也就是孩子数量=关键字数,而B树中,孩子数量=关键字数+1。
2,非叶子节点的关键字也会同时存在在子节点中,并且是在子节点中所有关键字的最大(或最小)。
3,非叶子节点仅用于索引,不保存数据记录,跟记录有关的信息都放在叶子节点中。而B树中,非叶子节点既保存索引,也保存数据记录。
4,所有关键字都在叶子节点出现,叶子节点构成一个有序链表,而且叶子节点本身按照关键字的大小从小到大顺序链接。
下图就是一棵B+树,阶数为3,根节点中的关键字1、18、35分别是子节点(1,8,14),(18,24,31)和(35,41,53)中的最小值。每一层父节点的关键字都会出现在下一层的子节点的关键字中,因此在叶子节点中包括了所有的关键字信息,并且每一个叶子节点都有一个指向下一个节点的指针,这样就形成了一个链表。
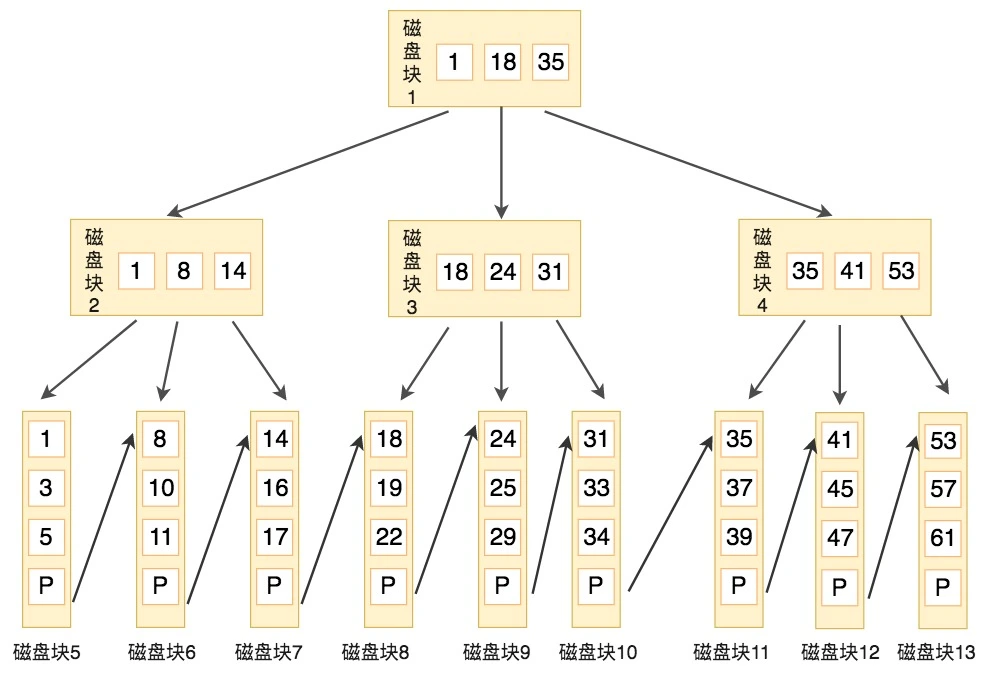
比如,我们想要查找关键字16,B+树会自顶向下逐层进行查找:
1,与根节点的关键字(1,18,35)进行比较,16在1和18之间,得到指针P1(指向磁盘块2)
2,找到磁盘块2,关键字为(1,8,14),因为16大于14,所以得到指针P3(指向磁盘块7)
3,找到磁盘块7,关键字为(14,16,17),然后我们找到了关键字16,所以可以找到关键字16所对应的数据。
整个过程一共进行了3次I/O操作,看起来B+树和B树的查询过程差不多,但是B+树和B树有个根本的差异在于,B+树的中间节点并不直接存储数据。这样的好处都有什么呢?
首先,B+树查询效率更稳定。因为B+树每次只有访问到叶子节点才能找到对应的数据,而在B树中,非叶子节点也会存储数据,这样就会造成查询效率不稳定的情况,有时候访问到了非叶子节点就可以找到关键字,而有时需要访问到叶子节点才能找到关键字。
其次,B+树的查询效率更高,这是因为通常B+树比B树更矮胖(阶数更大,深度更低),查询所需要的磁盘I/O也会更少。同样的磁盘页大小,B+树可以存储更多的节点关键字。
不仅是对单个关键字的查询上,在查询范围上,B+树的效率也比B树高。这是因为所有关键字都出现在B+树的叶子节点中,并通过有序链表进行了链接。而在B树中则需要通过中序遍历才能完成查询范围的查找,效率要低很多。
总结
磁盘的I/O操作次数对索引的使用效率至关重要。虽然传统的二叉树数据结构查找数据的效率高,但很容易增加磁盘I/O操作的次数,影响索引使用的效率。因此在构造索引的时候,我们更倾向于采用“矮胖”的数据结构。
B树和B+树都可以作为索引的数据结构,在MySQL中采用的是B+树,B+树在查询性能上更稳定,在磁盘页大小相同的情况下,树的构造更加矮胖,所需要进行的磁盘I/O次数更少,更适合进行关键字的范围查询。
今天我们对索引的底层数据结构进行了学习,你能说下为什么数据库索引采用B+树,而不是平衡二叉搜索树吗?另外,B+树和B树在构造和查询性能上有什么差异呢?