思考并回答以下问题:
- 层数是对节点而言的,高度是对树而言的。怎么理解?
- 前序遍历、中序遍历和后序遍历分别是什么样的?
本章知识点
- 理解树这种数据结构及其用法。
- 了解如何用树实现映射。
- 用类和引用实现树。
- 将树实现为递归数据结构。
- 用堆实现优先级队列。
术语及定义
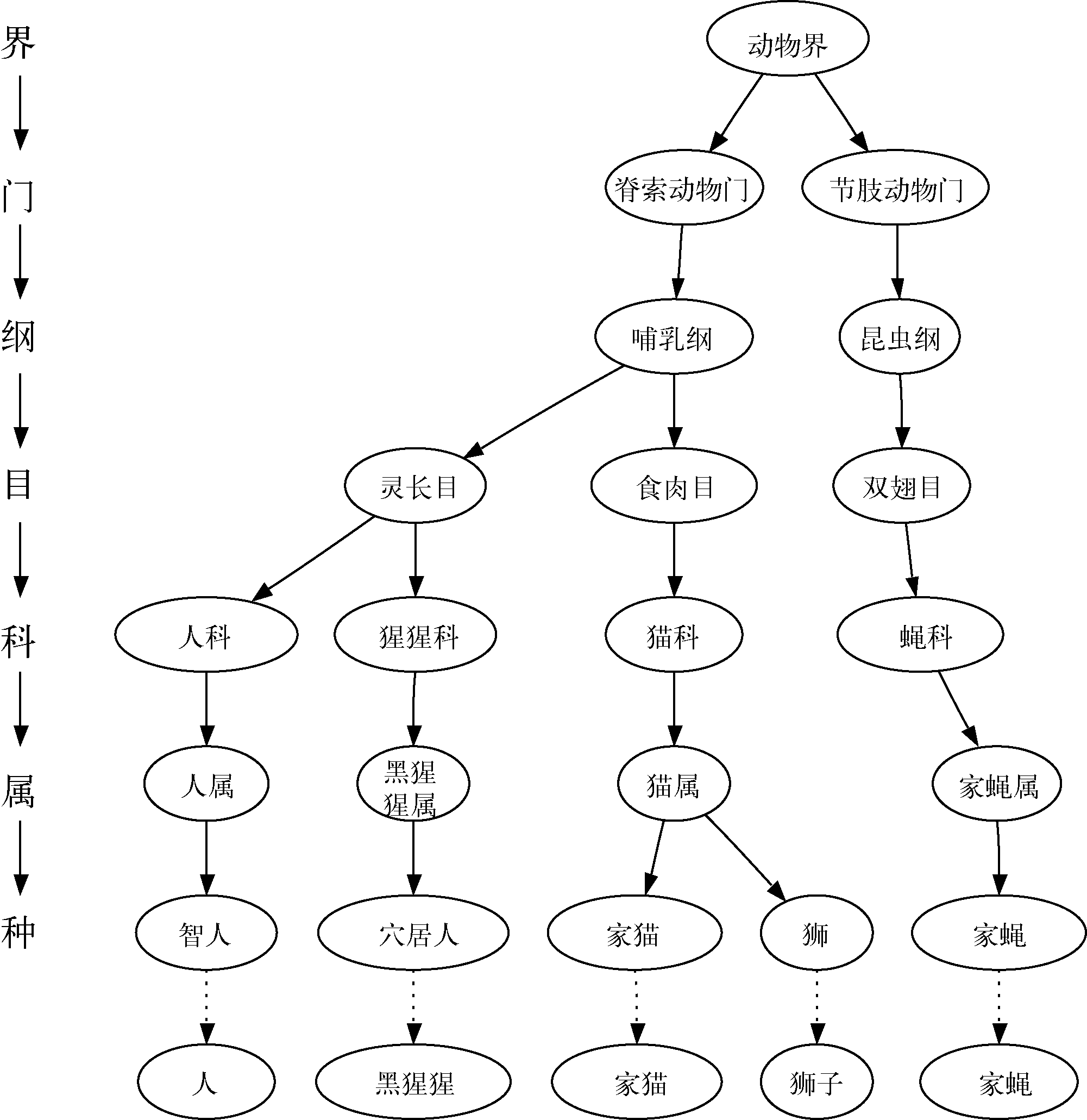
图1 用树表示一些常见动物的分类
树的属性
- 第一个属性是层次性,即树是按层级构建的,越笼统就越靠近顶部,越具体则越靠近底部。树的层次性衍生出另一个重要属性,即可以将树的某个部分(称作子树)整体移到另一个位置,而不影响下面的层。
- 树的第二个属性是,一个节点的所有子节点都与另一个节点的所有子节点无关。
- 第三个属性是,叶子节点都是独一无二的。
节点
节点是树的基础部分。它可以有自己的名字,我们称作“键”。节点也可以带有附加信息,我们称作“有效载荷”。有效载荷信息对于很多树算法来说不是重点,但它常常在使用树的应用中很重要。
边
边是树的另一个基础部分。两个节点通过一条边相连,表示它们之间存在关系。除了根节点以外,其他每个节点都仅有一条入边,出边则可能有多条。
根节点
根节点是树中唯一没有入边的节点。
路径
路径是由边连接的有序节点列表。
子节点
一个节点通过出边与子节点相连。
父节点
一个节点是其所有子节点的父节点。
兄弟节点
具有同一父节点的节点互称为兄弟节点。
子树
一个父节点及其所有后代的节点和边构成一棵子树。
叶子节点
叶子节点没有子节点。
层数
节点n的层数是从根节点到n的唯一路径长度。在图1中,猫属的层数是5。由定义可知,根节点的层数是 0。
高度
树的高度是其中节点层数的最大值。图1中的树高度为7。
树有两种定义,其中一种涉及节点和边,另一种涉及递归。你在后面会看到,递归定义很有用。
定义一:树由节点及连接节点的边构成。树有以下属性:
- 有一个根节点;
- 除根节点外,其他每个节点都与其唯一的父节点相连;
- 从根节点到其他每个节点都有且仅有一条路径;
- 如果每个节点最多有两个子节点,我们就称这样的树为二叉树。
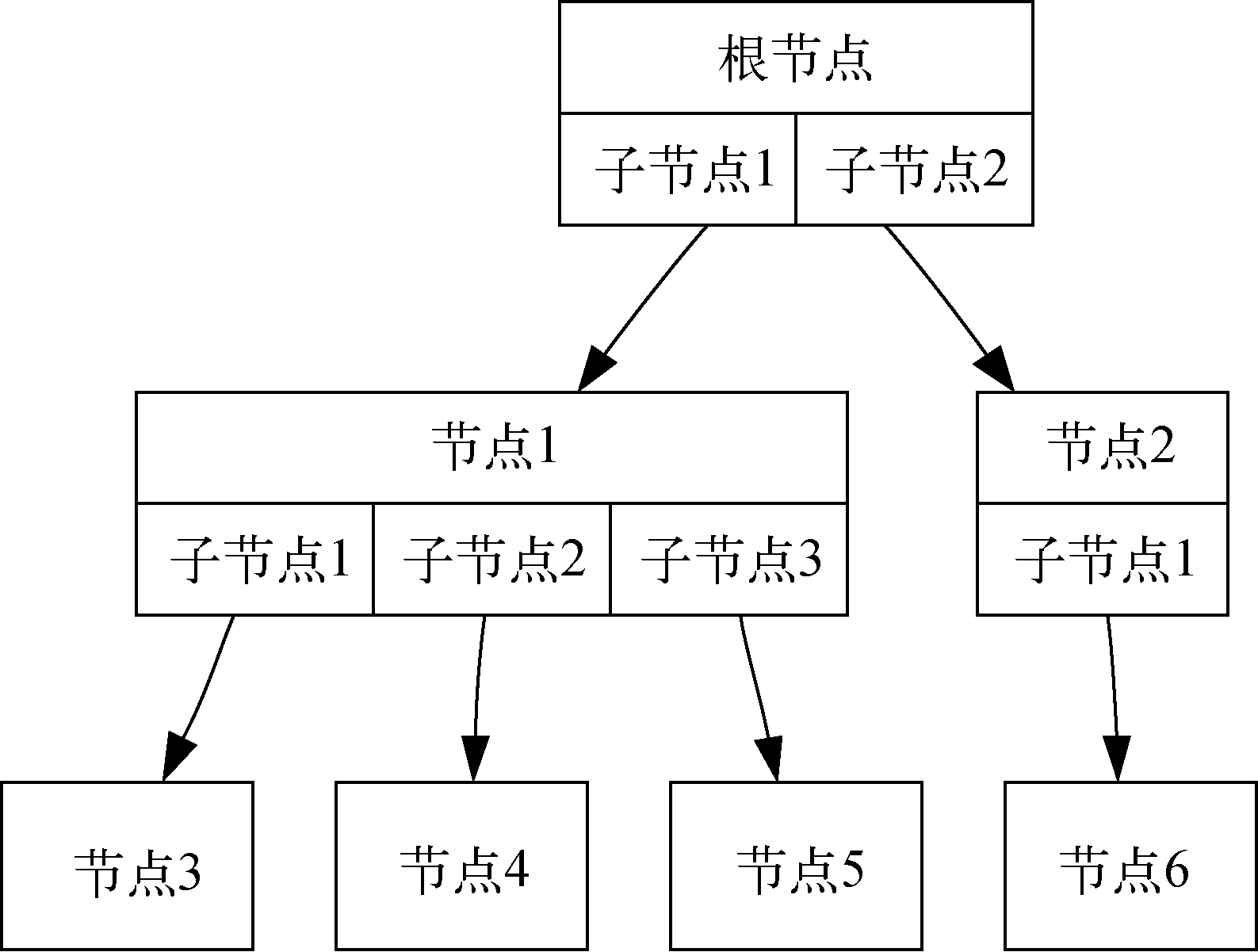
图2展示了一棵符合定义一的树。边的箭头表示连接方向。
图2 由节点和边构成的树
定义二:一棵树要么为空,要么由一个根节点和零棵或多棵子树构成,子树本身也是一棵树。每棵子树的根节点通过一条边连到父树的根节点。图3展示了树的递归定义。
图3 树的递归定义
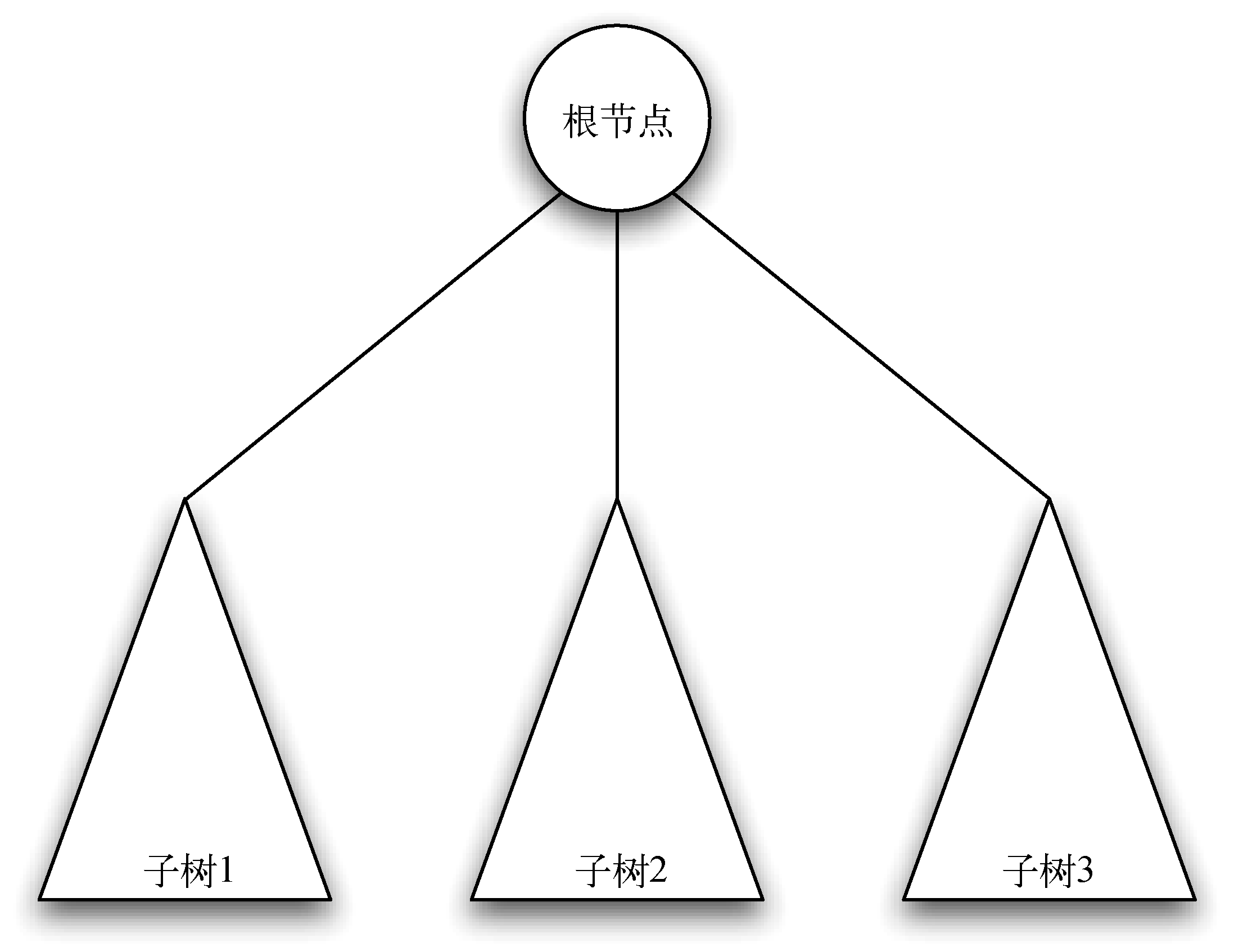
从树的递归定义可知,图中的树至少有4个节点,因为三角形代表的子树必定有一个根节点。这棵树或许有更多的节点,但必须更深入地查看子树后才能确定。
实现
根据上节给出的定义,可以使用以下函数创建并操作二叉树。
- BinaryTree() 创建一个二叉树实例。
- getLeftChild() 返回当前节点的左子节点所对应的二叉树。
- getRightChild() 返回当前节点的右子节点所对应的二叉树。
- setRootVal(val) 在当前节点中存储参数val中的对象。
- getRootVal() 返回当前节点存储的对象。
- insertLeft(val) 新建一棵二叉树,并将其作为当前节点的左子节点。
- insertRight(val) 新建一棵二叉树,并将其作为当前节点的右子节点。
我们将定义一个类,其中有根节点和左右子树的属性。
图3 “节点与引用”表示法的简单示例
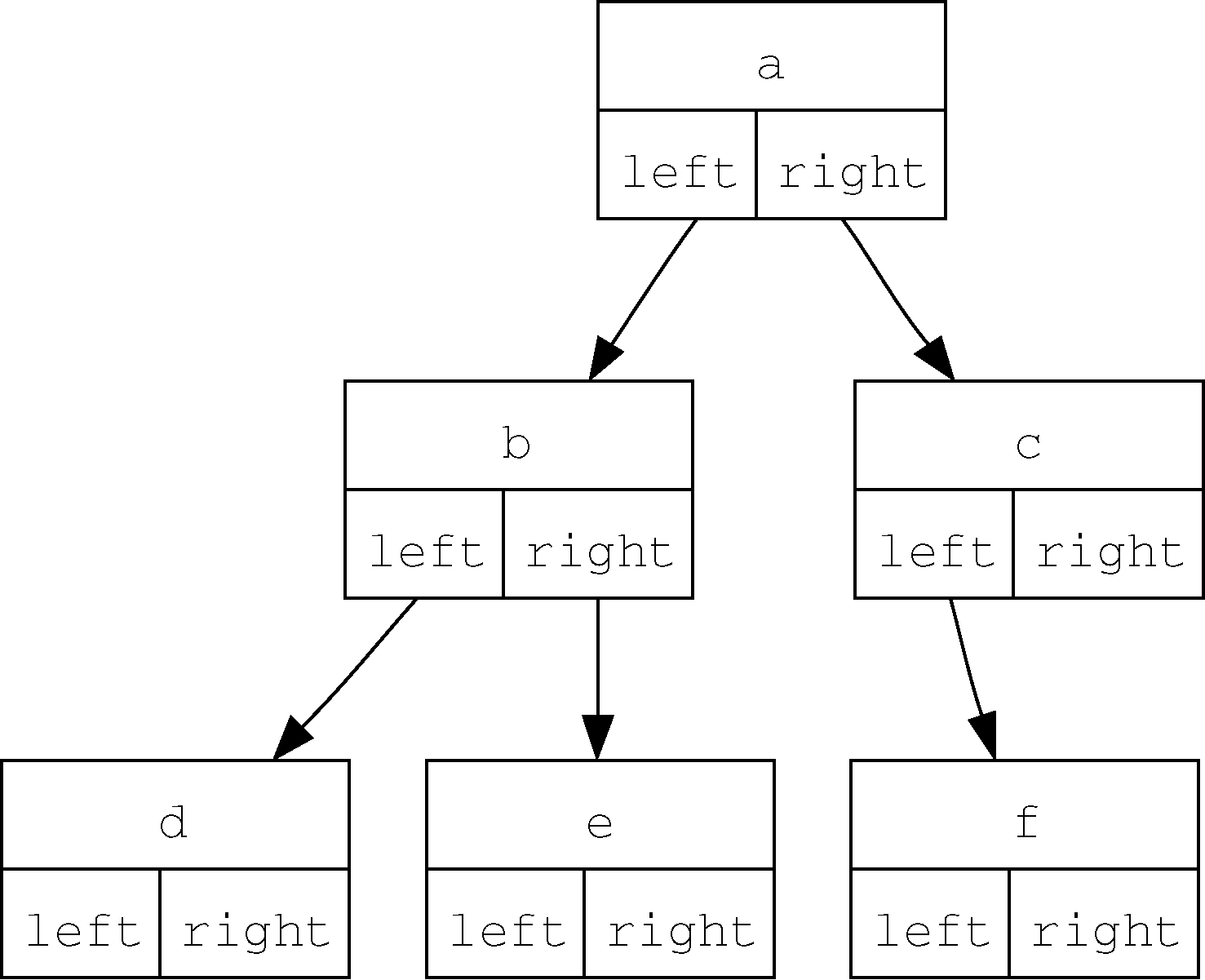
首先定义一个简单的类,如代码清单1所示。“节点与引用”表示法的要点是,属性left和right会指向BinaryTree类的其他实例。举例来说,在向树中插入新的左子树时,我们会创建另一个BinaryTree实例,并将根节点的self.leftChild改为指向新树。
代码清单1 BinaryTree类
1 | class BinaryTree: |
在代码清单1中,构造方法接受一个对象,并将其存储到根节点中。正如能在列表中存储任何对象,根节点对象也可以成为任何对象的引用。就之前的例子而言,我们将节点名作为根的值存储。采用“节点与引用”法表示图3中的树,将创建6个BinaryTree实例。
下面看看基于根节点构建树所需要的函数。为了给树添加左子树,我们新建一个二叉树对象,将根节点的left属性指向新对象。代码清单2给出了insertLeft函数的代码。
代码清单2 插入左子节点
1 | def insertLeft(self, newNode): |
在插入左子树时,必须考虑两种情况。第一种情况是原本没有左子节点。此时,只需往树中添加一个节点即可。第二种情况是已经存在左子节点。此时,插入一个节点,并将已有的左子节点降一层。代码清单2中的else语句处理的就是第二种情况。
insertRight函数也要考虑相应的两种情况:要么原本没有右子节点,要么必须在根节点和已有的右子节点之间插入一个节点。代码清单3给出了insertRight函数的代码。
代码清单3 插入右子节点
1 | def insertRight(self, newNode): |
为了完成对二叉树数据结构的定义,我们来编写一些访问左右子节点与根节点的函数,如代码清单4所示。
代码清单4 二叉树的访问函数
1 | def getRightChild(self): |
有了创建与操作二叉树的所有代码,现在用它们来进一步了解结构。我们创建一棵简单的树,并为根节点a添加子节点b和c。下面的Python会话创建了这棵树,并查看key、left和right中存储的值。注意,根节点的左右子节点本身都是BinaryTree类的实例。正如递归定义所言,二叉树的所有子树也都是二叉树。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20from pythonds.trees import BinaryTree
r = BinaryTree('a')
r.getRootVal()
'a'
print(r.getLeftChild())
None
r.insertLeft('b')
print(r.getLeftChild())
<__main__.BinaryTree instance at 0x6b238>
print(r.getLeftChild().getRootVal())
b
r.insertRight('c')
print(r.getRightChild())
<__main__.BinaryTree instance at 0x6b9e0>
print(r.getRightChild().getRootVal())
c
r.getRightChild().setRootVal('hello')
print(r.getRightChild().getRootVal())
hello
>>>
二叉树的应用
解析树
树的实现已经齐全了,现在来看看如何用树解决一些实际问题。本节介绍解析树,可以用它来表示现实世界中像句子(如图4所示)或数学表达式这样的构造。
图4 一个简单句子的解析树
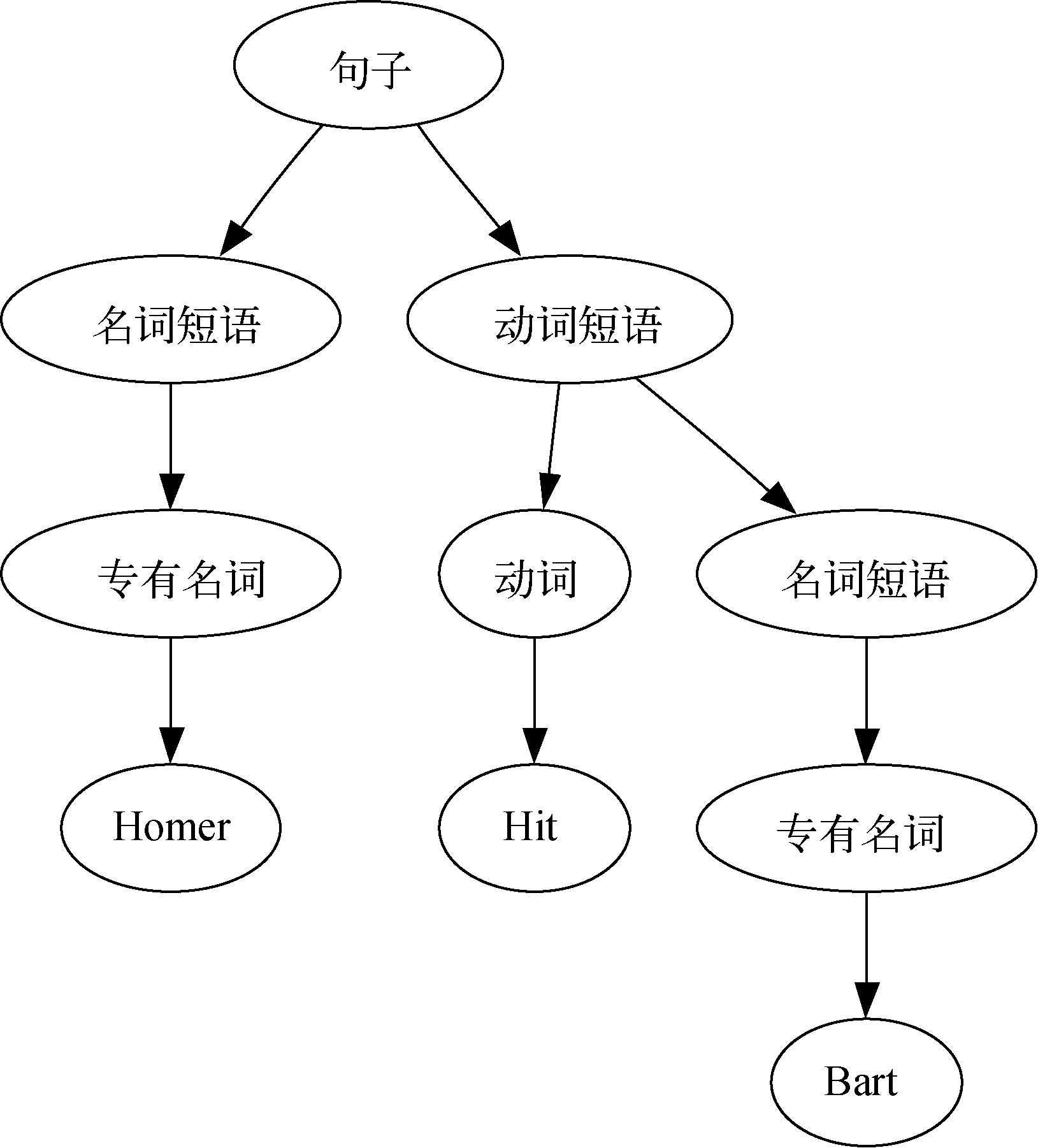
图4展示了一个简单句子的层次结构。用树状结构表示句子让我们可以使用子树处理句子的独立部分。
我们也可以将((7 + 3) * (5 - 2))这样的数学表达式表示成解析树,如图5所示。
图5 ((7 + 3) * (5 - 2))的解析树
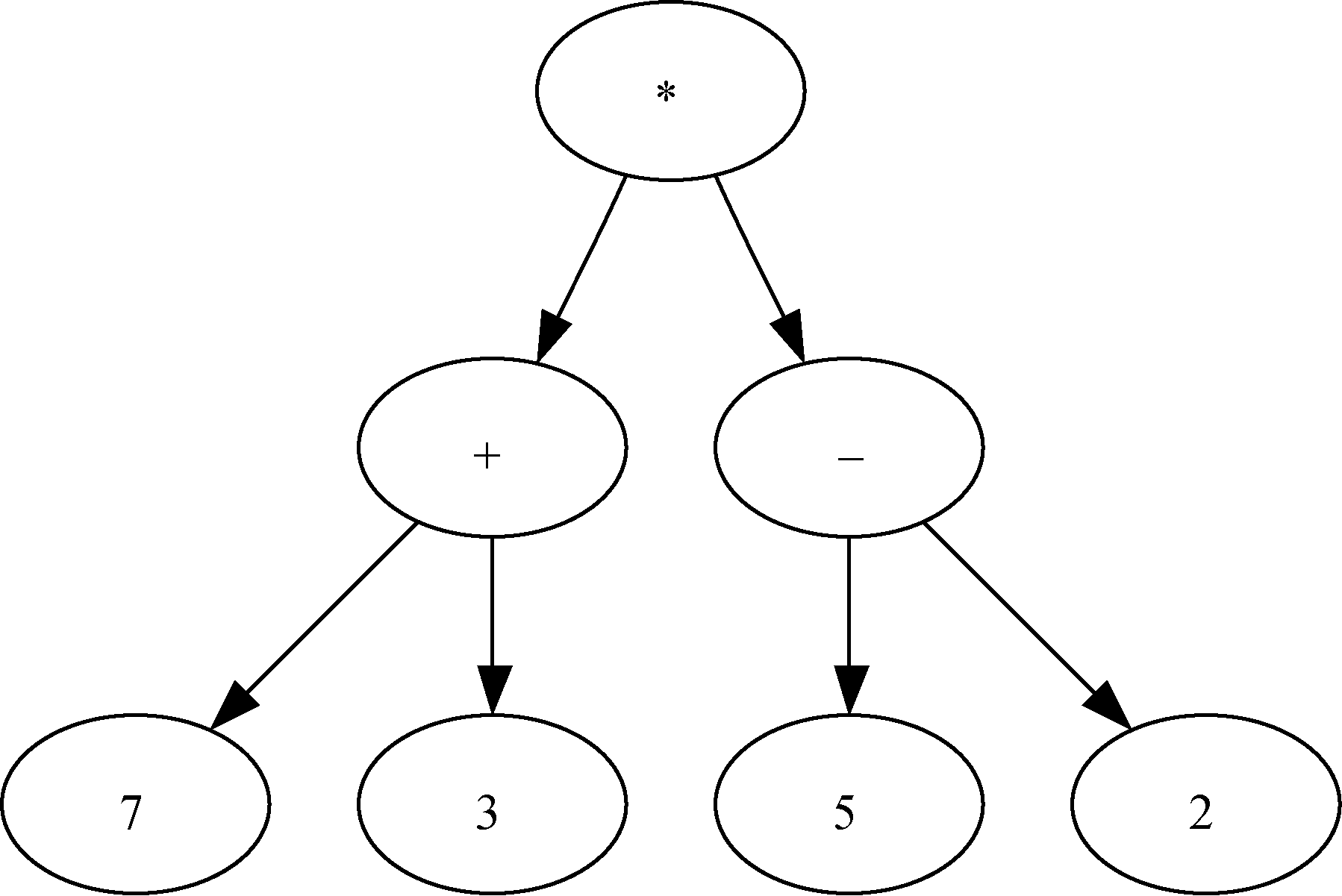
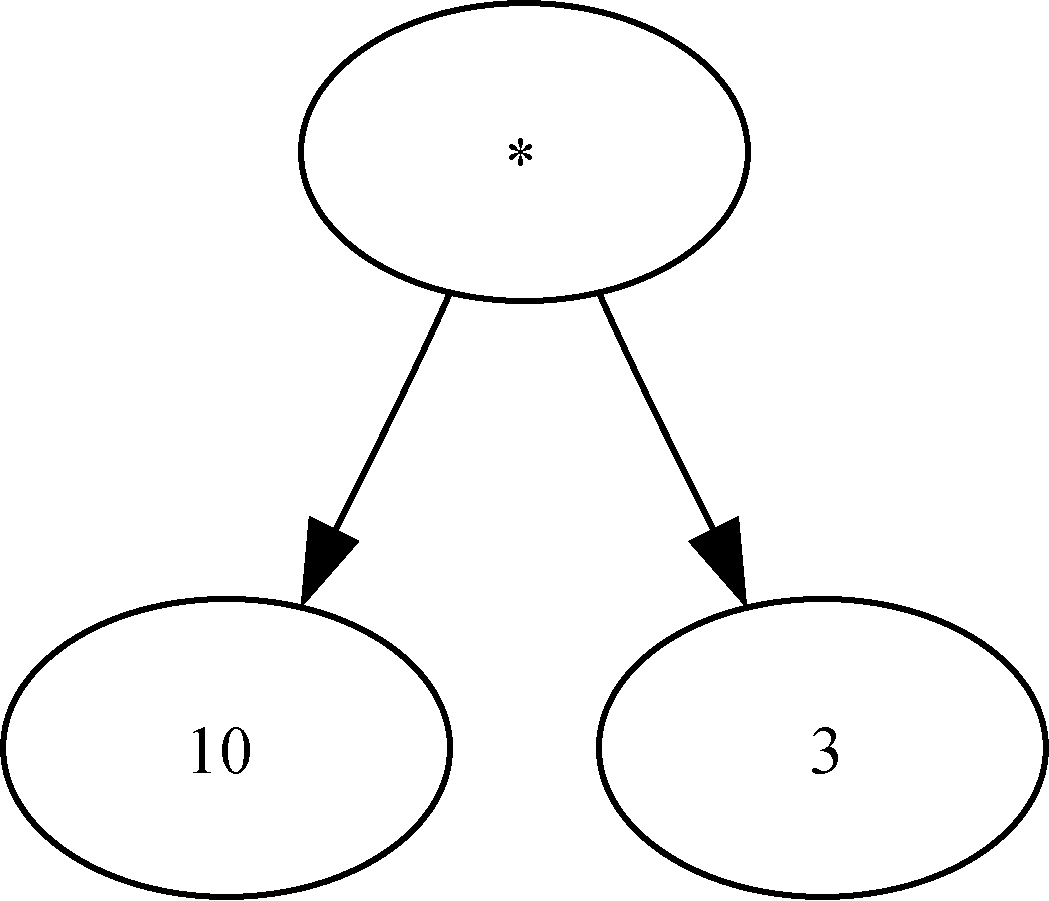
这是完全括号表达式,乘法的优先级高于加法和减法,但因为有括号,所以在做乘法前必须先做括号内的加法和减法。树的层次性有助于理解整个表达式的计算次序。在计算顶层的乘法前,必须先计算子树中的加法和减法。加法(左子树)的结果是10,减法(右子树)的结果是3。利用树的层次结构,在计算完子树的表达式后,只需用一个节点代替整棵子树即可。应用这个替换过程后,便得到如图6所示的简化树。
图6 ((7 + 3) * (5 - 2))的简化解析树
本节的剩余部分将仔细考察解析树,重点如下:
- 如何根据完全括号表达式构建解析树;
- 如何计算解析树中的表达式;
- 如何将解析树还原成最初的数学表达式。
构建解析树的第一步是将表达式字符串拆分成标记列表。需要考虑4种标记:左括号、右括号、运算符和操作数。我们知道,左括号代表新表达式的起点,所以应该创建一棵对应该表达式的新树。反之,遇到右括号则意味着到达该表达式的终点。我们也知道,操作数既是叶子节点,也是其运算符的子节点。此外,每个运算符都有左右子节点。
有了上述信息,便可以定义以下4条规则:
- (1) 如果当前标记是(,就为当前节点添加一个左子节点,并下沉至该子节点;
- (2) 如果当前标记在列表[‘+’, ‘-‘, ‘/‘, ‘*‘]中,就将当前节点的值设为当前标记对应的运算符;为当前节点添加一个右子节点,并下沉至该子节点;
- (3) 如果当前标记是数字,就将当前节点的值设为这个数并返回至父节点;
- (4) 如果当前标记是),就跳到当前节点的父节点。
编写Python代码前,我们先通过一个例子来理解上述规则。将表达式(3 + (4 * 5))拆分成标记列表[‘(‘, ‘3’, ‘+’, ‘(‘, ‘4’, ‘*‘, ‘5’, ‘)’, ‘)’]。起初,解析树只有一个空的根节点,随着对每个标记的处理,解析树的结构和内容逐渐充实,如图7所示。
图7 一步步地构建解析树

以图7为例,我们来一步步地构建解析树。
(a) 创建一棵空树。
(b) 读入第一个标记(。根据规则1,为根节点添加一个左子节点。
(c) 读入下一个标记3。根据规则3,将当前节点的值设为3,并回到父节点。
(d) 读入下一个标记+。根据规则2,将当前节点的值设为+,并添加一个右子节点。新节点成为当前节点。
(e) 读入下一个标记(。根据规则1,为当前节点添加一个左子节点,并将其作为当前节点。
(f) 读入下一个标记4。根据规则3,将当前节点的值设为4,并回到父节点。
(g) 读入下一个标记*。根据规则2,将当前节点的值设为*,并添加一个右子节点。新节点成为当前节点。
(h) 读入下一个标记5。根据规则3,将当前节点的值设为5,并回到父节点。
(i) 读入下一个标记)。根据规则4,将*的父节点作为当前节点。
(j) 读入下一个标记)。根据规则4,将+的父节点作为当前节点。因为+没有父节点,所以工作完成。
本例表明,在构建解析树的过程中,需要追踪当前节点及其父节点。可以通过getLeftChild与getRightChild获取子节点,但如何追踪父节点呢?一个简单的办法就是在遍历这棵树时使用栈记录父节点。每当要下沉至当前节点的子节点时,先将当前节点压到栈中。当要返回到当前节点的父节点时,就将父节点从栈中弹出来。
利用前面描述的规则以及Stack和BinaryTree,就可以编写创建解析树的Python函数。代码清单5给出了解析树构建器的代码。
代码清单5 解析树构建器
1 | from pythonds.basic import Stack |
在代码清单5中,第11、15、19和24行的if语句体现了构建解析树的4条规则,其中每条语句都通过调用BinaryTree和Stack的方法实现了前面描述的规则。这个函数中唯一的错误检查在else从句中,如果遇到一个不能识别的标记,就抛出一个ValueError异常。
有了一棵解析树之后,我们能对它做些什么呢?作为第一个例子,我们可以写一个函数计算解析树,并返回计算结果。要写这个函数,我们将利用树的层次性。针对图7中的解析树,可以用图8中的简化解析树替换。由此可见,可以写一个算法,通过递归计算每棵子树得到整棵解析树的结果。
和之前编写递归函数一样,设计递归计算函数要从确定基本情况开始。就针对树进行操作的递归算法而言,一个很自然的基本情况就是检查叶子节点。解析树的叶子节点必定是操作数。由于像整数和浮点数这样的数值对象不需要进一步翻译,因此evaluate函数可以直接返回叶子节点的值。为了向基本情况靠近,算法将执行递归步骤,即对当前节点的左右子节点调用evaluate函数。递归调用可以有效地沿着各条边往叶子节点靠近。
若要结合两个递归调用的结果,只需将父节点中存储的运算符应用于子节点的计算结果即可。从图8中可知,根节点的两个子节点的计算结果就是它们自身,即10和3。应用乘号,得到最后的结果30。
递归函数evaluate的实现如代码清单10所示。首先,获取指向当前节点的左右子节点的引用。如果左右子节点的值都是None,就说明当前节点确实是叶子节点。第7行执行这项检查。如果当前节点不是叶子节点,则查看当前节点中存储的运算符,并将其应用于左右子节点的递归计算结果。
代码清单6 计算二叉解析树的递归函数
1 | def evaluate(parseTree): |
我们使用具有键+、-、*和/的字典实现。字典中存储的值是operator模块的函数。该模块给我们提供了常用运算符的函数版本。在字典中查询运算符时,对应的函数对象被取出。既然取出的对象是函数,就可以用普通的方式function(param1, param2)调用。因此,opers[\‘+\‘](2, 2)等价于operator.add(2, 2)。
最后,让我们通过图9中的解析树构建过程来理解evaluate函数。第一次调用evaluate函数时,将整棵树的根节点作为参数parseTree传入。然后,获取指向左右子节点的引用,检查它们是否存在。第9行进行递归调用。从查询根节点的运算符开始,该运算符是+,对应operator.add函数,要传入两个参数。和普通的Python函数调用一样,Python做的第一件事是计算入参的值。本例中,两个入参都是对evaluate函数的递归调用。由于入参的计算顺序是从左到右,因此第一次递归调用是在左边。对左子树递归调用evaluate函数,发现节点没有左右子节点,所以这是一个叶子节点。处于叶子节点时,只需返回叶子节点的值作为计算结果即可。本例中,返回整数3。
至此,我们已经为顶层的operator.add调用计算出一个参数的值了,但还没完。继续从左到右的参数计算过程,现在进行一个递归调用,计算根节点的右子节点。我们发现,该节点不仅有左子节点,还有右子节点,所以检查节点存储的运算符——是*,将左右子节点作为参数调用函数。这时可以看到,两个调用都已到达叶子节点,计算结果分别是4和5。算出参数之后,返回operator.mul(4, 5)的结果。至此,我们已经算出了顶层运算符(+)的操作数,剩下的工作就是完成对operator.add(3, 20)的调用。因此,表达式(3 + (4 * 5))的计算结果就是23。
树的遍历
我们将对所有节点的访问称为“遍历”,共有3种遍历方式,分别为前序遍历、中序遍历和后序遍历。接下来,我们先仔细地定义这3种遍历方式,然后通过一些例子看看它们的用法。
前序遍历
在前序遍历中,先访问根节点,然后递归地前序遍历左子树,最后递归地前序遍历右子树。
中序遍历
在中序遍历中,先递归地中序遍历左子树,然后访问根节点,最后递归地中序遍历右子树。
后序遍历
在后序遍历中,先递归地后序遍历右子树,然后递归地后序遍历左子树,最后访问根节点。
首先看看前序遍历。我们将一本书的内容结构表示为一棵树,整本书是根节点,每一章是根节点的子节点,每一章中的每一节是这章的子节点,每小节又是这节的子节点,依此类推。图10展示了一本书的树状结构,它包含两章。
图10 一本书的树状结构
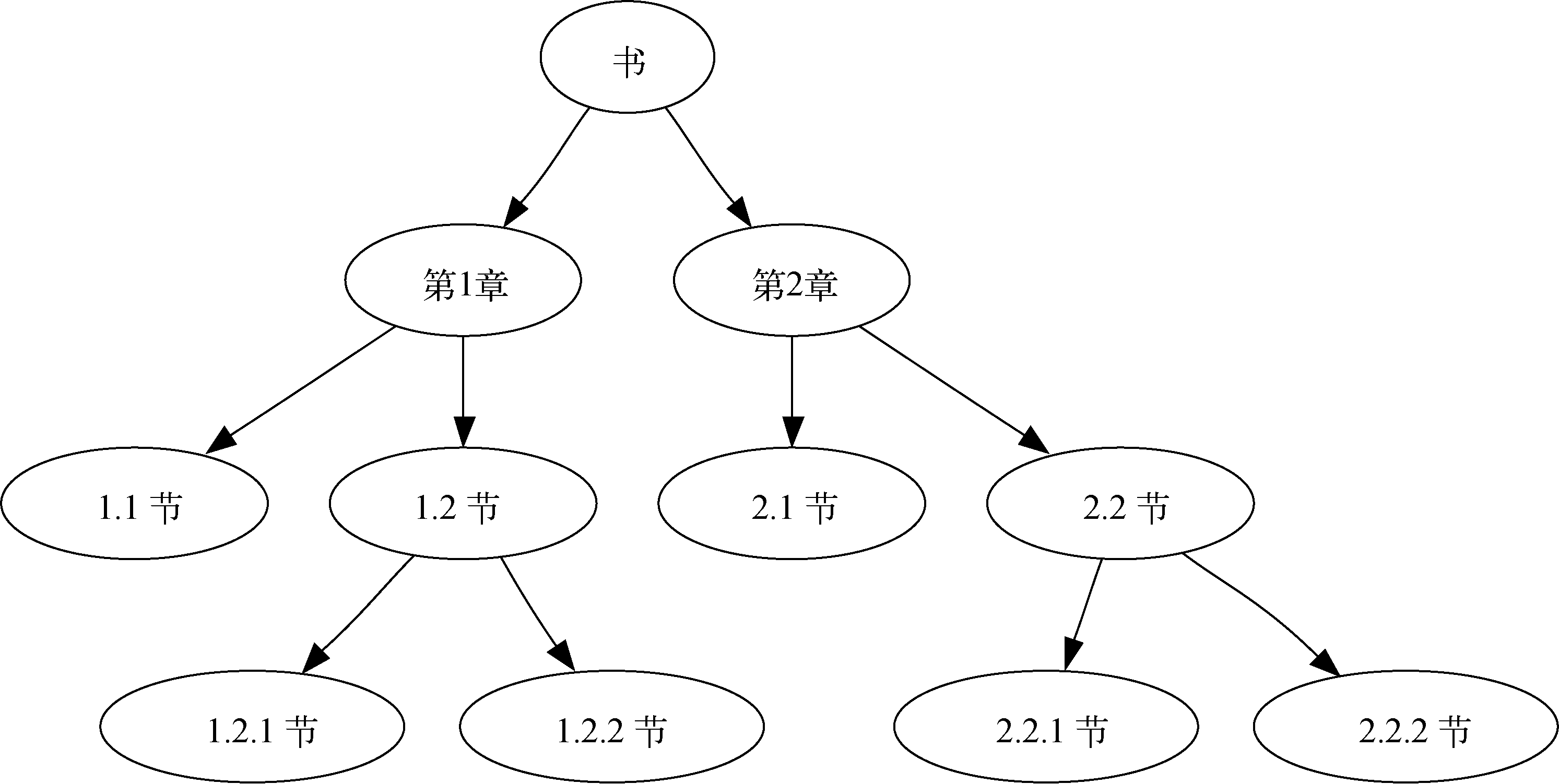
假设我们从前往后阅读这本书,那么阅读顺序就符合前序遍历的次序。从根节点“书”开始,遵循前序遍历指令,对左子节点“第1章”递归调用preorder函数。然后,对“第1章”的左子节点递归调用preorder函数,得到节点“1.1节”。由于该节点没有子节点,因此不必再进行递归调用。沿着树回到节点“第1章”,接下来访问它的右子节点,即“1.2节”。和前面一样,先访问左子节点“1.2.1节”,然后访问右子节点“1.2.2节”。访问完“1.2节”之后,回到“第1章”。接下来,回到根节点,以同样的方式访问节点“第2章”。
遍历树的代码格外简洁,这主要是因为遍历是递归的。
你可能会想,前序遍历算法的最佳实现方式是什么呢?是一个将树用作数据结构的函数,还是树本身的一个方法?代码清单11给出了前序遍历算法的外部函数版本,该函数将二叉树作为参数,其代码尤为简洁,这是因为算法的基本情况仅仅是检查树是否存在。如果参数tree是None,函数直接返回。
代码清单11 将前序遍历算法实现为外部函数
1 | def preorder(tree): |
我们也可以将preorder实现为BinaryTree类的方法,如代码清单12所示。请留意将代码从外部移到内部后有何变化。通常来说,不仅需要用self代替tree,还需要修改基本情况。内部方法必须在递归调用preorder前,检查左右子节点是否存在。
代码清单12 将前序遍历算法实现为BinaryTree类的方法
1 | def preorder(self): |
哪种实现方式更好呢?在本例中,将preorder实现为外部函数可能是更好的选择。原因在于,很少会仅执行遍历操作,在大多数情况下,还要通过基本的遍历模式实现别的目标。在下一个例子中,我们就会通过后序遍历来计算解析树。所以,我们在此采用外部函数版本。
在代码清单13中,后序遍历函数postorder与前序遍历函数preorder几乎相同,只不过对print的调用被移到了函数的末尾。
代码清单13 后序遍历函数
1 | def postorder(tree): |
我们已经见识过后序遍历的一个常见用途,那就是计算解析树。回顾代码清单10,我们所做的就是先计算左子树,再计算右子树,最后通过根节点运算符的函数调用将两个结果结合起来。假设二叉树只存储一个表达式的数据。让我们来重写计算函数,使之更接近于代码清单13中的后序遍历函数。
代码清单14 后序求值函数
1 | def postordereval(tree): |
注意,代码清单14与代码清单13在形式上很相似,只不过求值函数最后不是打印节点,而是返回节点。这样一来,就可以保存从第7行和第8行的递归调用返回的值,然后在第10行使用这些值和运算符进行计算。
最后来了解中序遍历。中序遍历的访问顺序是左子树、根节点、右子树。代码清单15给出了中序遍历函数的代码。注意,3个遍历函数的区别仅在于print语句与递归调用语句的相对位置。
代码清单15 中序遍历函数
1 | def inorder(tree): |
通过中序遍历解析树,可以还原不带括号的表达式。接下来修改中序遍历算法,以得到完全括号表达式。唯一要做的修改是:在递归调用左子树前打印一个左括号,在递归调用右子树后打印一个右括号。代码清单16是修改后的函数。
代码清单16 修改后的中序遍历函数,它能还原完全括号表达式
1 | def printexp(tree): |
以下Python会话展示了printexp和postordereval的用法。1
2
3
4
5
6
7
8
9
10
11
12
13
14from pythonds.trees import BinaryTree
x = BinaryTree('*')
x.insertLeft('+')
l = x.getLeftChild()
l.insertLeft(4)
l.insertRight(5)
x.insertRight(7)
>>>
print(printexp(x))
(((4) + (5)) * (7))
>>>
print(postordereval(x))
63
>>>
注意,printexp函数给每个数字都加上了括号。尽管不能算错误,但这些括号显然是多余的。在章末的练习中,请修改printexp函数,移除这些括号。
利用二叉堆实现优先级队列
第3章介绍过队列这一先进先出的数据结构。队列有一个重要的变体,叫作优先级队列。和队列一样,优先级队列从头部移除元素,不过元素的逻辑顺序是由优先级决定的。优先级最高的元素在最前,优先级最低的元素在最后。因此,当一个元素入队时,它可能直接被移到优先级队列的头部。你在第7章会看到,对于一些图算法来说,优先级队列是一个有用的数据结构。
你或许可以想到一些使用排序函数和列表实现优先级队列的简单方法。但是,就时间复杂度而言,列表的插入操作是O(n),排序操作是O(n log n)。其实,效率可以更高。实现优先级队列的经典方法是使用叫作二叉堆的数据结构。二叉堆的入队操作和出队操作均可达到O(log n)。
二叉堆学起来很有意思,它画出来很像一棵树,但实现时只用一个列表作为内部表示。二叉堆有两个常见的变体:最小堆(最小的元素一直在队首)与最大堆(最大的元素一直在队首)。
本节将实现最小堆,并将最大堆的实现留作练习。
二叉堆的操作
我们将实现以下基本的二叉堆方法。
- BinaryHeap()新建一个空的二叉堆。
- insert(k)往堆中加入一个新元素。
- findMin()返回最小的元素,元素留在堆中。
- delMin()返回最小的元素,并将该元素从堆中移除。
- isEmpty()在堆为空时返回True,否则返回False。
- size()返回堆中元素的个数。
- buildHeap(list)根据一个列表创建堆。
以下 Python会话展示了一些二叉堆方法的用法。1
2
3
4
5
6
7
8
9
10
11
12
13from pythonds.trees import BinaryHeap
bh = BinaryHeap()
bh.insert(5)
bh.insert(7)
bh.insert(3)
bh.insert(11)
print(bh.delMin())
3
print(bh.delMin())
5
print(bh.delMin())
7
print(bh.delMin())
二叉堆的实现
1.结构属性
为了使二叉堆能高效地工作,我们利用树的对数性质来表示它。你会在6.7.3节学到,为了保证对数性能,必须维持树的平衡。平衡的二叉树是指,其根节点的左右子树含有数量大致相等的节点。在实现二叉堆时,我们通过创建一棵完全二叉树来维持树的平衡。在完全二叉树中,除了最底层,其他每一层的节点都是满的。在最底层,我们从左往右填充节点。图11展示了完全二叉树的一个例子。
图11 完全二叉树
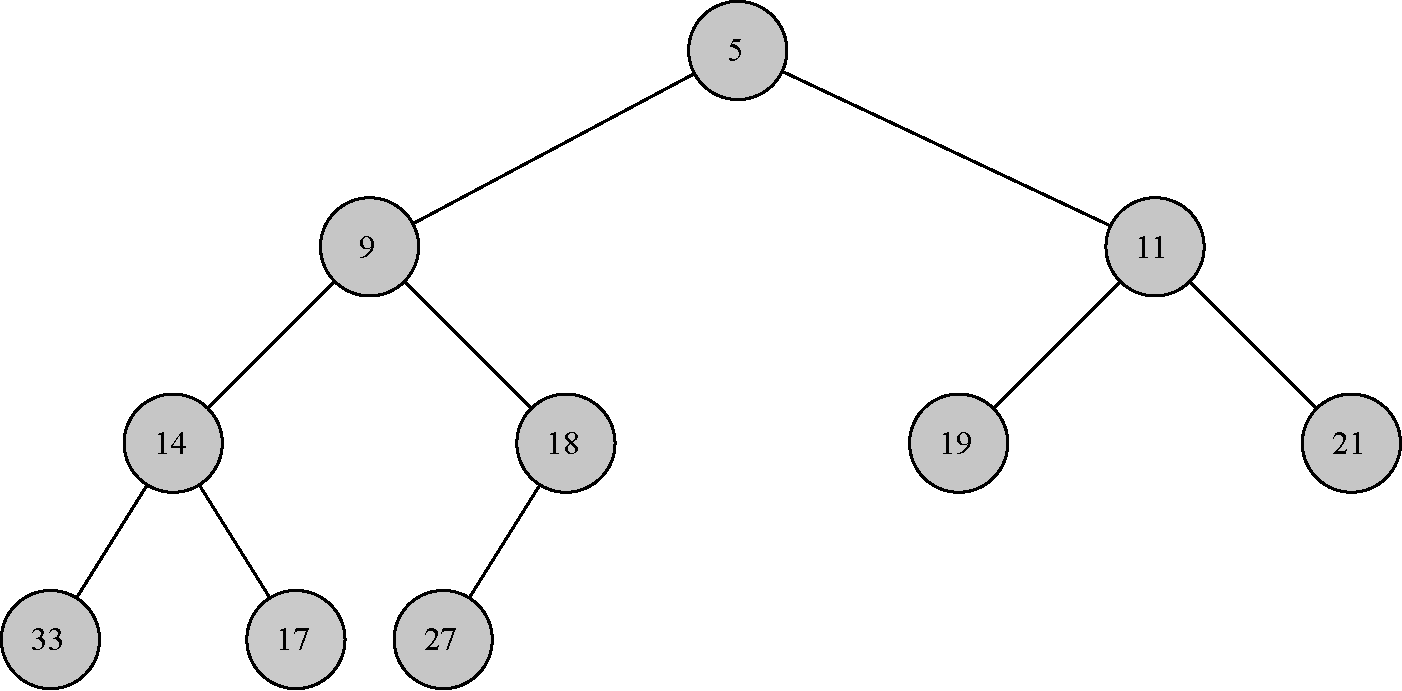
完全二叉树的另一个有趣之处在于,可以用一个列表来表示它,而不需要采用“列表之列表”或“节点与引用”表示法。由于树是完全的,因此对于在列表中处于位置p的节点来说,它的左子节点正好处于位置2p;同理,右子节点处于位置2p+1。若要找到树中任意节点的父节点,只需使用Python的整数除法即可。给定列表中位置 n处的节点,其父节点的位置就是 n/2。图6-15展示了一棵完全二叉树,并给出了列表表示。树的列表表示——加上这个“完全”的结构性质——让我们得以通过一些简单的数学运算遍历完全二叉树。我们会看到,这也有助于高效地实现二叉堆。
图12 一棵完全二叉树及其列表表示
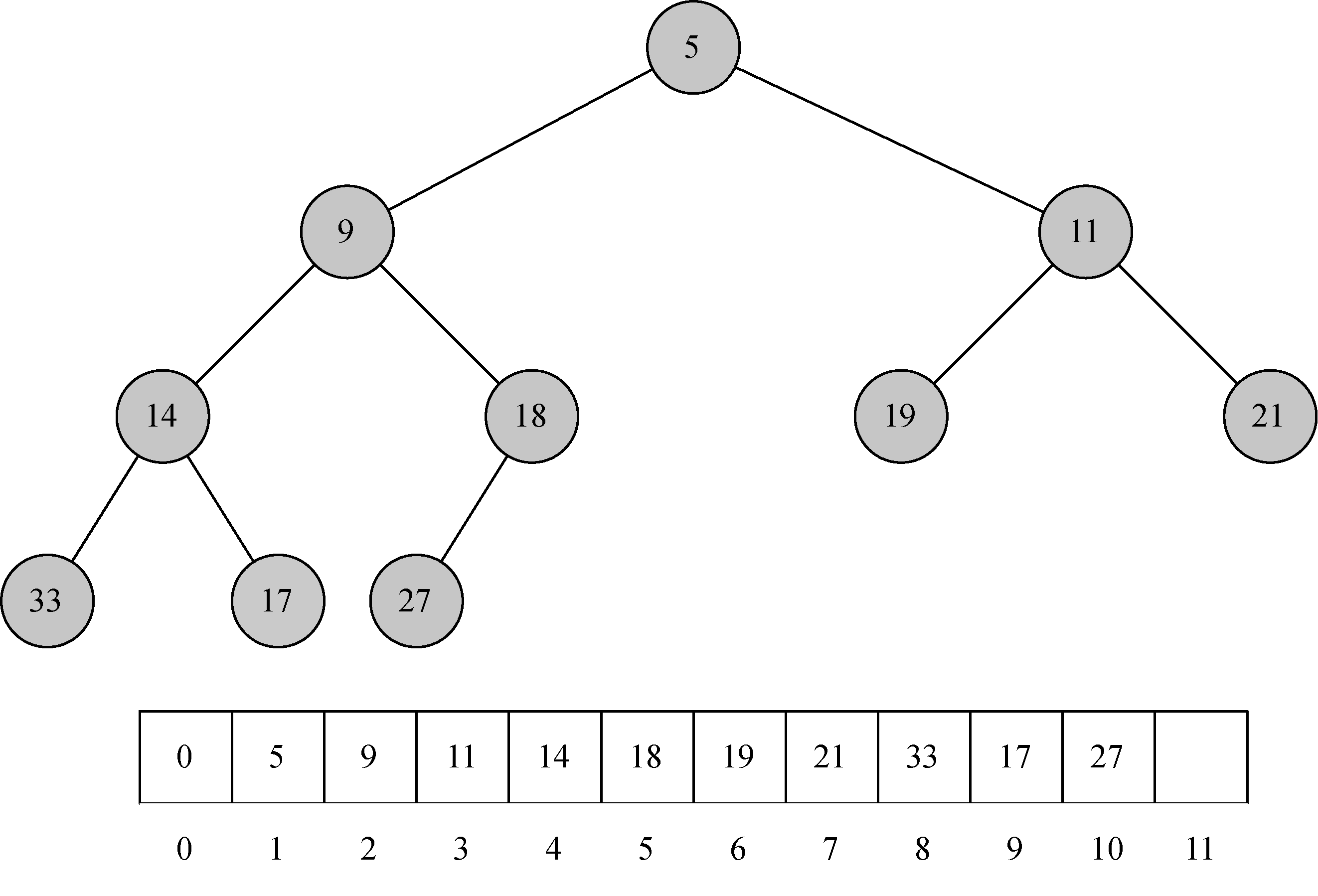
2.堆的有序性
我们用来存储堆元素的方法依赖于堆的有序性。堆的有序性是指:对于堆中任意元素x及其父元素p,p都不大于x。图12也展示出完全二叉树具备堆的有序性。
3.堆操作
首先实现二叉堆的构造方法。既然用一个列表就可以表示整个二叉堆,那么构造方法要做的就是初始化这个列表与属性currentSize,用于记录堆的当前大小。代码清单17给出了构造方法的Python代码。列表heapList的第一个元素是0,它的唯一用途是为了使后续的方法可以使用整数除法。
代码清单17 新建二叉堆
1 | def __init__(self): |
接下来实现insert方法。将元素加入列表的最简单、最高效的方法就是将元素追加到列表的末尾。追加操作的优点在于,它能保证完全树的性质,但缺点是很可能会破坏堆的结构性质。
不过可以写一个方法,通过比较新元素与其父元素来重新获得堆的结构性质。如果新元素小于其父元素,就将二者交换。图16展示了将新元素放到正确位置上所需的一系列交换操作。
图13 将新元素往上移到正确位置
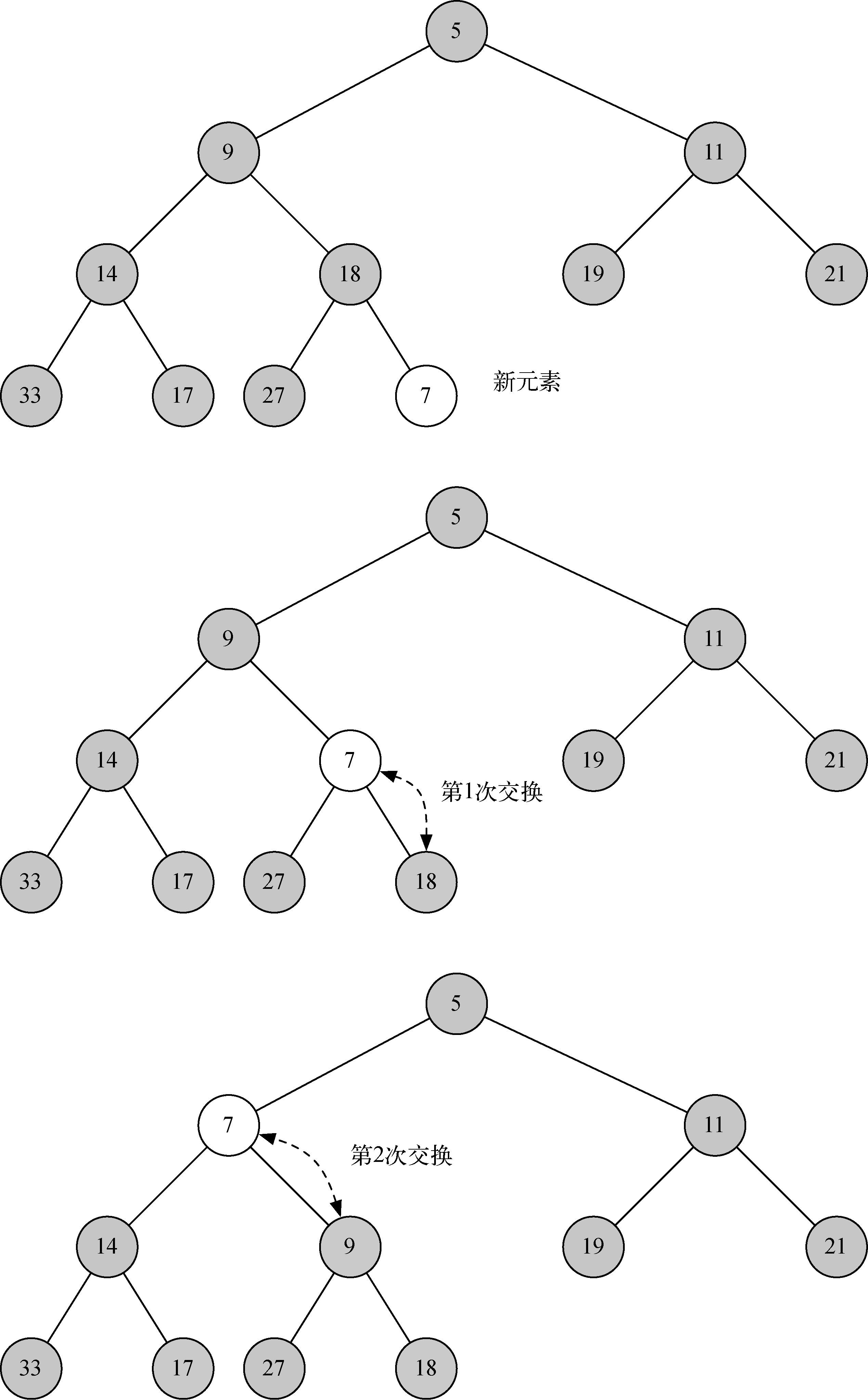
注意,将元素往上移时,其实是在新元素及其父元素之间重建堆的结构性质。此外,也保留了兄弟元素之间的堆性质。当然,如果新元素很小,需要继续往上一层交换。代码清单18给出了percUp方法的代码,该方法将元素一直沿着树向上移动,直到重获堆的结构性质。此时,heapList中的元素0正好能发挥重要作用。我们使用整数除法计算任意节点的父节点。就当前节点而言,父节点的下标就是当前节点的下标除以2。
代码清单18 percUp方法
1 | def percUp(self, i): |
现在准备好编写insert方法了。代码清单19给出了该方法的Python代码。其实,insert方法的大部分工作是由percUp方法完成的。当元素被追加到树中之后,percUp方法将其移到正确的位置。
代码清单19 向二叉堆中新加元素
1 | def insert(self, k): |
正确定义insert方法后,就可以编写delMin方法。既然堆的结构性质要求根节点是树的最小元素,那么查找最小值就很简单。delMin方法的难点在于,如何在移除根节点之后重获堆的结构性质和有序性。可以分两步重建堆。第一步,取出列表中的最后一个元素,将其移到根节点的位置。移动最后一个元素保证了堆的结构性质,但可能会破坏二叉堆的有序性。第二步,将新的根节点沿着树推到正确的位置,以重获堆的有序性。图6-17展示了将新的根节点移动到正确位置所需的一系列交换操作。
图14 将根节点往下移到正确位置
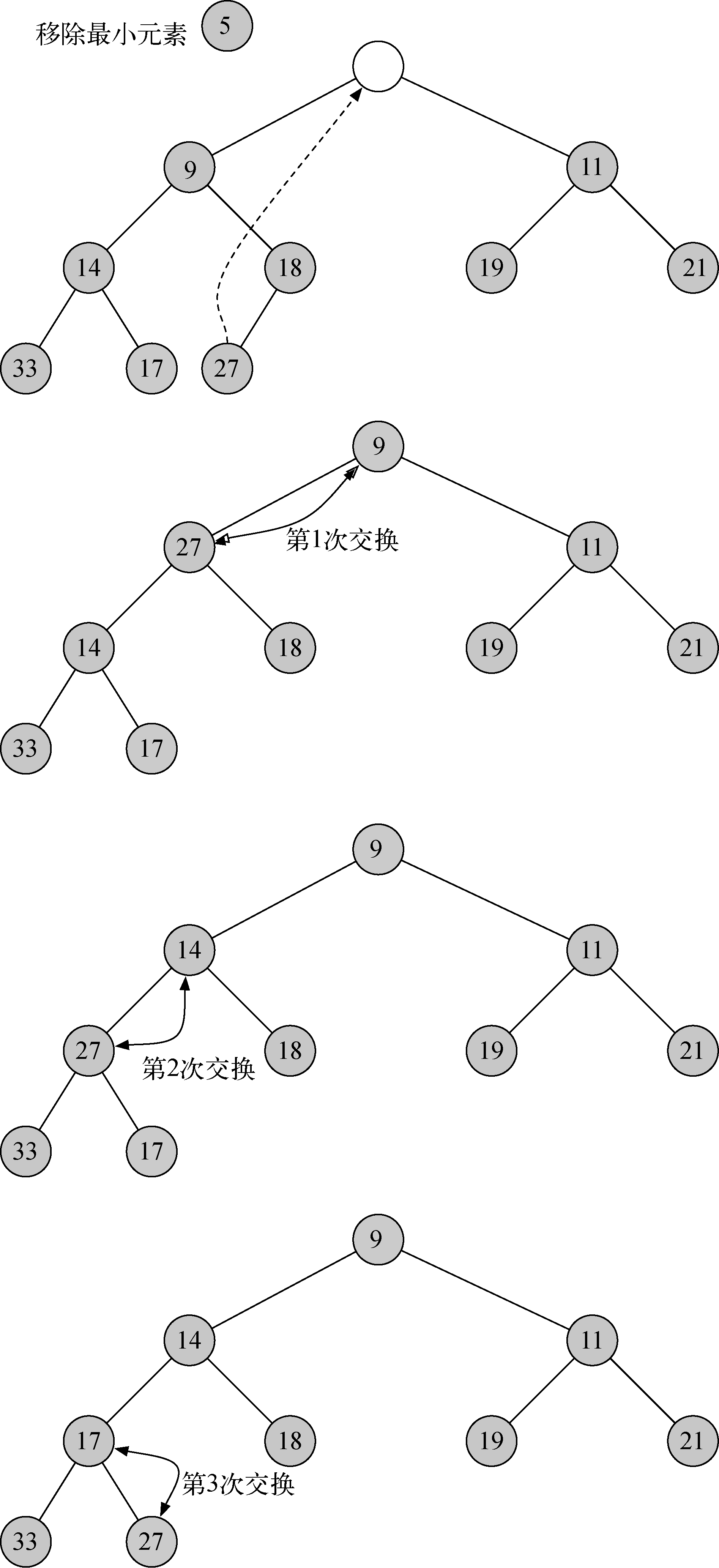
为了维持堆的有序性,只需交换根节点与它的最小子节点即可。重复节点与子节点的交换过程,直到节点比其两个子节点都小。代码清单20给出了percDown方法和minChild方法的Python代码。
代码清单20 percDown方法和minChild方法
1 | def percDown(self, i): |
delMin方法如代码清单21所示。同样,主要工作也由辅助函数完成。本例中的辅助函数是percDown。
代码清单21 从二叉堆中删除最小的元素
1 | def delMin(self): |
关于二叉堆,还有最后一点需要讨论。我们来看看根据元素列表构建整个堆的方法。你首先想到的方法或许是这样的:给定元素列表,每次插入一个元素,构建一个堆。由于是从列表只有一个元素的情况开始,并且列表是有序的,因此可以采用二分搜索算法找到下一个元素的正确插入位置,时间复杂度约为O(log n)。但是,为了在列表的中部插入元素,可能需要移动其他元素,以为新元素腾出空间,这种操作的时间复杂度为O(n)。因此,将n个元素插入堆中的操作为O(n log n)。然而,如果从完整的列表开始,构建整个堆只需O(n)。代码清单22给出了构建整个堆的代码。
代码清单22 根据元素列表构建堆
1 | def buildHeap(self, alist): |
图15 根据列表[9, 6, 5, 2, 3]构建堆
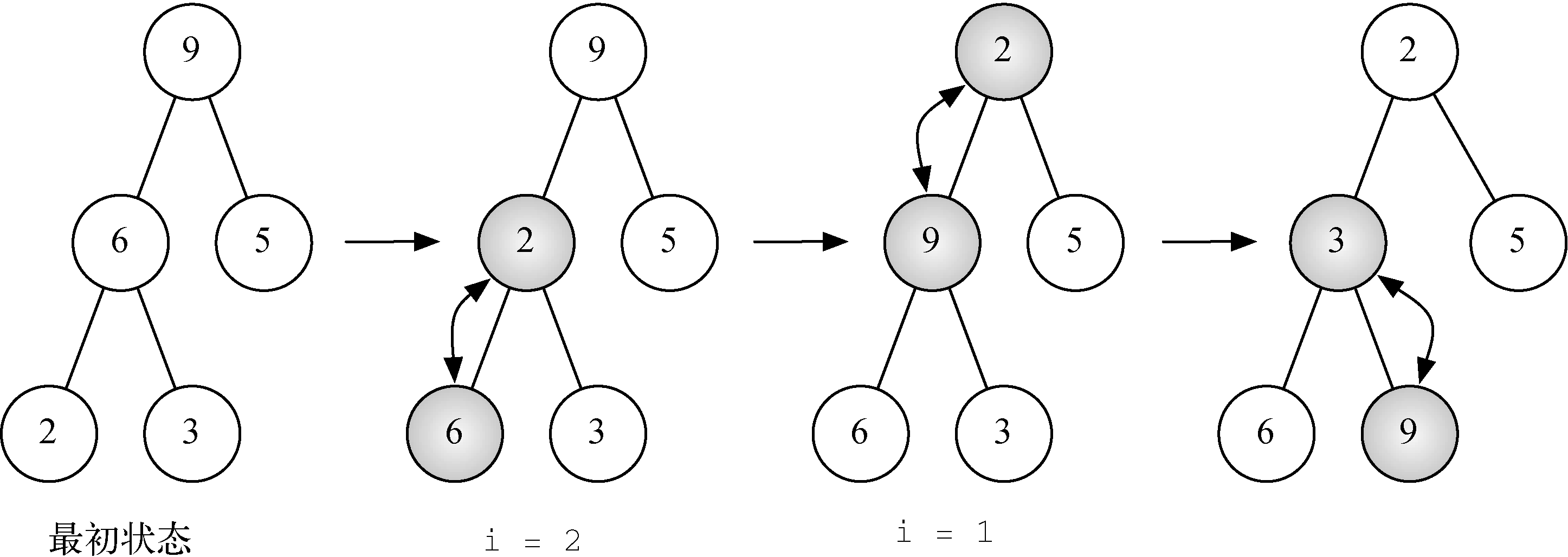
图15展示了buildHeap方法进行的交换过程,它将各节点从最初状态移到各自的正确位置上。尽管从树的中间开始,向根的方向操作,但是percDown方法保证了最大的节点总是沿着树向下移动。在这棵完全二叉树中,超过中点的节点都是叶子节点,没有任何子节点。当i=1时,从树的根节点往下移,可能需要经过多次交换。如你所见,9先被移出根节点,然后percDown会沿着树检查子节点,以确保尽量将它往下移。在本例中,9的第2次交换对象是3。这样一来,9就移到了树的底层,不需要再做交换了。比较一系列交换操作后的列表表示将有助于理解,如图16所示。
图16 根据列表[9, 6, 5, 2, 3]构建堆
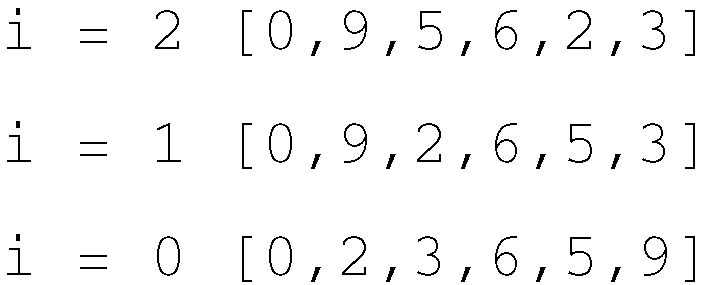
前面说过,构建堆的时间复杂度是O(n),这乍一听可能很难理解,证明过程超出了本书范畴。不过,要点在于,因子log n是由树的高度决定的。在buildHeap的大部分工作中,树的高度不足log n。
利用建堆的时间复杂度为O(n)这一点,可以构造一个使用堆为列表排序的算法,使它的时间复杂度为O(n log n)。这个算法留作练习。
二叉搜索树
我们已经学习了两种从集合中获取键–值对的方法。回想一下,我们讨论过映射抽象数据类型的两种实现,它们分别是列表二分搜索和散列表。本节将探讨二叉搜索树,它是映射的另一种实现。我们感兴趣的不是元素在树中的确切位置,而是如何利用二叉树结构提供高效的搜索。
搜索树的操作
在实现搜索树之前,我们来复习一下映射抽象数据类型提供的接口。你会发现,这个接口类似于Python字典。
- Map()新建一个空的映射。
- put(key, val)往映射中加入一个新的键–值对。如果键已经存在,就用新值替换旧值。
- get(key)返回key对应的值。如果key不存在,则返回None。
- del通过del map[key]这样的语句从映射中删除键–值对。
- len()返回映射中存储的键–值对的数目。
- in通过key in map这样的语句,在键存在时返回True,否则返回False 。
搜索树的实现
二叉搜索树依赖于这样一个性质:小于父节点的键都在左子树中,大于父节点的键则都在右子树中。我们称这个性质为二叉搜索性,它会引导我们实现上述映射接口。图6-20描绘了二叉搜索树的这个性质,图中只展示了键,没有展示对应的值。注意,每一对父节点和子节点都具有这个性质。左子树的所有键都小于根节点的键,右子树的所有键则都大于根节点的键。
图6-20 简单的二叉搜索树
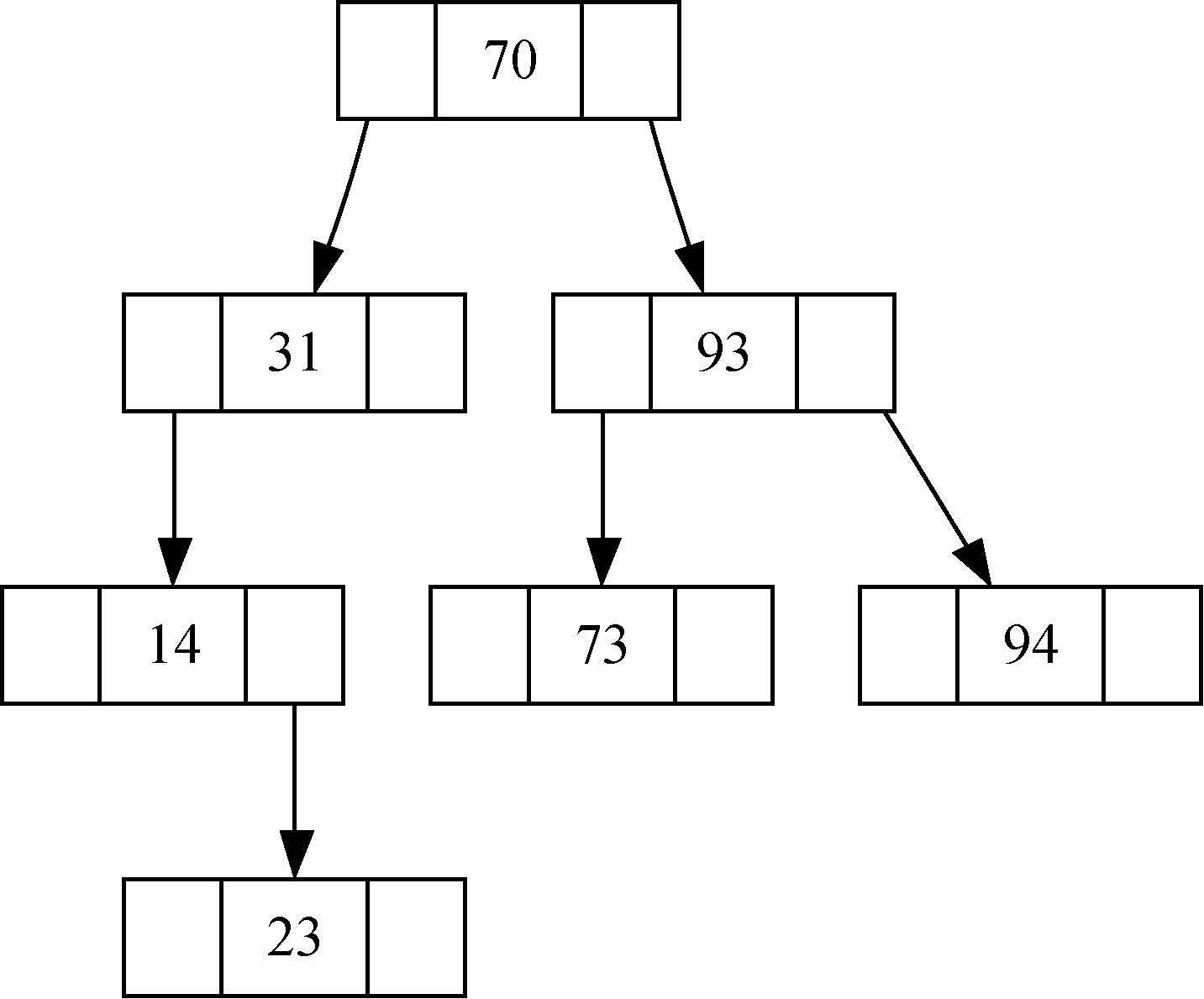
接下来看看如何构造二叉搜索树。图6-20中的节点是按如下顺序插入键之后形成的:70、31、93、94、14、23、73。因为70是第一个插入的键,所以是根节点。31小于70,所以成为70的左子节点。93大于70,所以成为70的右子节点。现在树的两层已经满了,所以下一个键会成为31或93的子节点。94比70和93都要大,所以它成了93的右子节点。同理,14比70和31都要小,所以它成了31的左子节点。23也小于31,所以它必定在31的左子树中。而它又大于14,所以成了14的右子节点。
我们将采用“节点与引用”表示法实现二叉搜索树,它类似于我们在实现链表和表达式树时采用的方法。不过,由于必须创建并处理一棵空的二叉搜索树,因此我们将使用两个类。一个称作BinarySearchTree,另一个称作TreeNode。BinarySearchTree类有一个引用,指向作为二叉搜索树根节点的TreeNode类。大多数情况下,外面这个类的方法只是检查树是否为空。如果树中有节点,请求就被发往BinarySearchTree类的私有方法,这个方法以根节点作为参数。当树为空,或者想删除根节点的键时,需要采取特殊措施。代码清单23是BinarySearchTree类的构造方法及一些其他的方法。
代码清单23 BinarySearchTree类
1 | class BinarySearchTree: |
TreeNode类提供了很多辅助函数,这大大地简化了BinarySearchTree类的工作。代码清单24是TreeNode类的构造方法以及辅助函数。可以看到,很多辅助函数有助于根据子节点的位置(是左还是右)以及自己的子节点类型来给节点归类。
代码清单24 TreeNode类
1 | class TreeNode: |
TreeNode类与6.4.2节中的BinaryTree类有一个很大的区别,那就是显式地将每个节点的父节点记录为它的一个属性。在讨论del操作的实现时,你会看到这一点为何重要。
在TreeNode类的实现中,另一个有趣之处是使用Python的可选参数。可选参数使得在多种环境下创建TreeNode更方便。有时,我们想构造一个已有parent和child的TreeNode。可以将父节点和子节点作为参数传入。其他时候,只通过键–值对创建TreeNode,而不传入parent和child。在这种情况下,可选参数使用默认值。
现在有了BinarySearchTree和TreeNode,是时候写一个帮我们构建二叉搜索树的put方法了。put是BinarySearchTree类的一个方法。它检查树是否已经有根节点,若没有,就创建一个TreeNode,并将其作为树的根节点;若有,就调用私有的递归辅助函数_put,并根据以下算法在树中搜索。
- 从根节点开始搜索二叉树,比较新键与当前节点的键。如果新键更小,搜索左子树。如果新键更大,搜索右子树。
- 当没有可供搜索的左(右)子节点时,就说明找到了新键的插入位置。
- 向树中插入一个节点,做法是创建一个TreeNode对象,并将其插入到前一步发现的位置上。
向树中插入新节点的方法如代码清单25所示。按照上述步骤,我们将_put写成递归函数。注意,在向树中插入新的子节点时,currentNode被作为父节点传入新树。
代码清单25 为二叉搜索树插入新节点
1 | def put(self, key, val): |
插入方法有个重要的问题:不能正确地处理重复的键。遇到重复的键时,它会在已有节点的右子树中创建一个具有同样键的节点。这样做的结果就是搜索时永远发现不了较新的键。要处理重复键插入,更好的做法是用关联的新值替换旧值。这个修复工作留作练习。
定义put方法后,就可以方便地通过让__setitem__方法调用put方法来重载[]运算符。如此一来,就可以写出像myZipTree[‘Plymouth’] = 55446这样的Python语句,就如同访问Python字典一样。__setitem__方法如代码清单26所示。
代码清单26 _setitem_方法
1 | def __setitem__(self, k, v): |
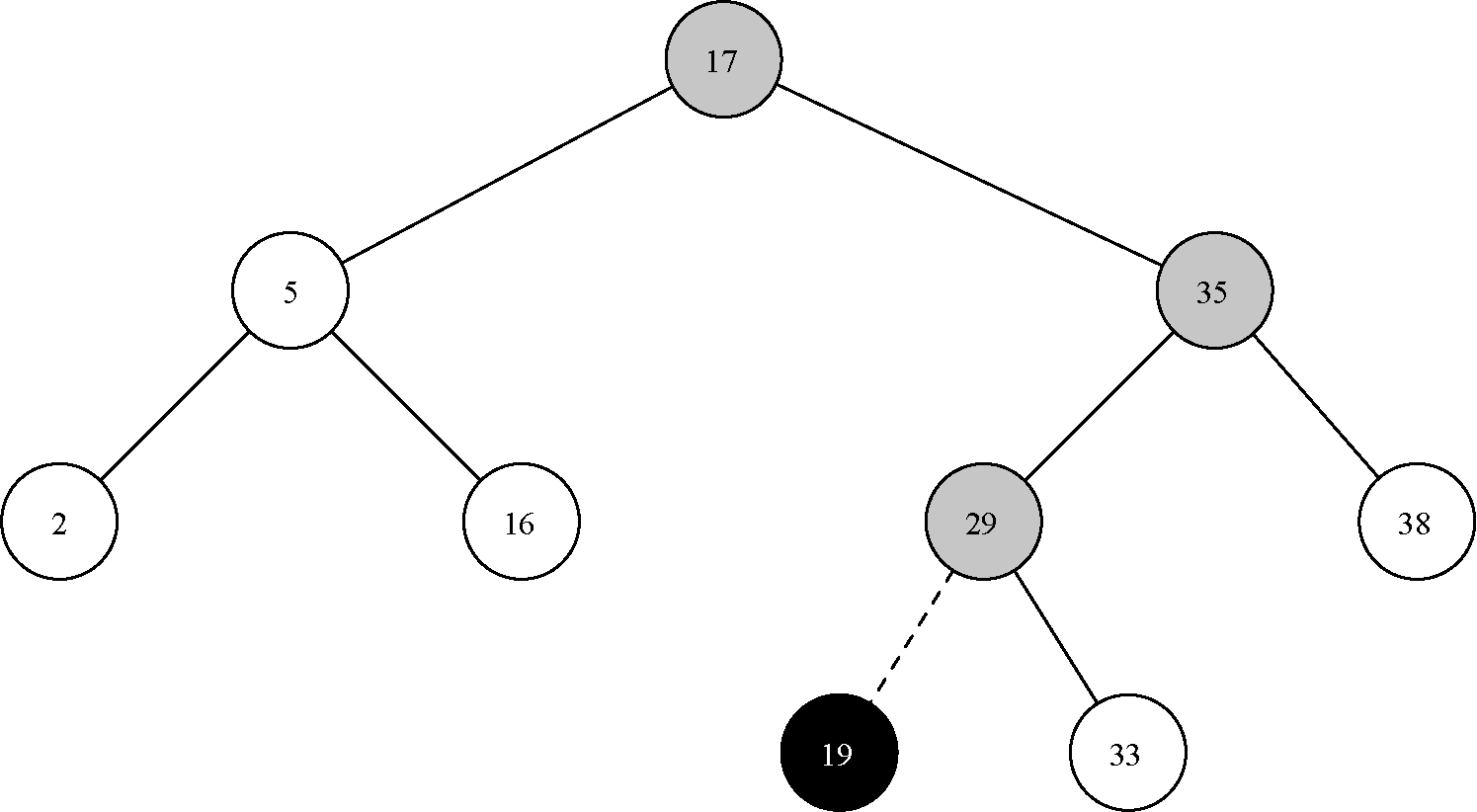
图6-21展示了向二叉搜索树中插入新节点的过程。浅灰色节点表示在插入过程中被访问过的节点。
构造出树后,下一个任务就是实现为给定的键取值。get方法比put方法还要简单,因为它只是递归地搜索二叉树,直到访问到叶子节点或者找到匹配的键。在后一种情况下,它会返回节点中存储的值。
图6-21 插入键为19的新节点
get、_get和__getitem__的实现如代码清单27所示。_get方法中的搜索代码和_put方法中选择左右子节点的逻辑相同。注意,_get方法返回一个TreeNode给get。这样一来,对于其他BinarySearchTree方法来说,如果需要使用TreeNode有效载荷之外的数据,_get可以作为灵活的辅助函数使用。
通过实现__getitem__方法,可以写出类似于访问字典的Python语句——而实际上使用的是二叉搜索树——比如z = myZipTree[‘Fargo’]。从代码清单27可以看出,__getitem__方法要做的就是调用get方法。
代码清单27 查找键对应的值
1 | def get(self, key): |
利用get方法,可以通过为BinarySearchTree编写_contains方法来实现in操作。\contains方法只需调用get方法,并在get方法返回一个值时返回True,或在get方法返回None时返回False。代码清单28实现了\contains_方法。
代码清单28 检查树中是否有某个键
1 | def __contains__(self, key): |
你应该记得,_contains_方法重载了in运算符,因此我们可以写出这样的语句:1
2if 'Northfield' in myZipTree:
print("oom ya ya")
最后,我们将注意力转向二叉搜索树中最有挑战性的方法——删除一个键。第一个任务是在树中搜索并找到要删除的节点。如果树中不止一个节点,使用_get方法搜索,找到要移除的TreeNode。如果树中只有一个节点,则意味着要移除的是根节点,不过仍要确保根节点的键就是要删除的键。无论哪种情况,如果找不到要删除的键,delete方法都会抛出一个异常,如代码清单29所示。
代码清单29 delete方法
1 | def delete(self, key): |
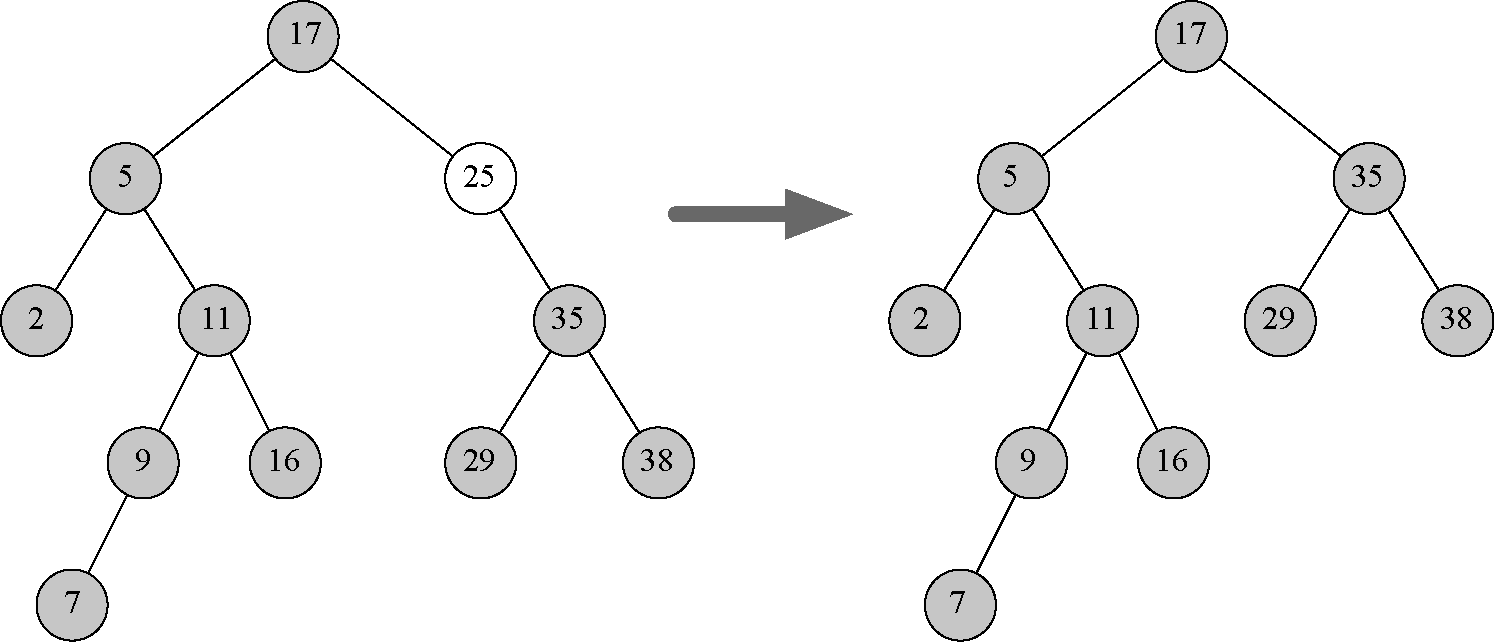
一旦找到待删除键对应的节点,就必须考虑3种情况。
(1)待删除节点没有子节点(如图22所示)。
图6-22 待删除节点16没有子节点
(2)待删除节点只有一个子节点(如图23所示)。
图6-23 待删除节点25有一个子节点
(3)待删除节点有两个子节点(如图24所示)。
图6-24 待删除节点5有两个子节点
情况1很简单。如果当前节点没有子节点,要做的就是删除这个节点,并移除父节点对这个节点的引用,如代码清单30所示。
代码清单30 情况1:待删除节点没有子节点
1 | if currentNode.isLeaf(): |
情况2稍微复杂些。如果待删除节点只有一个子节点,那么可以用子节点取代待删除节点,如代码清单31所示。查看这段代码后会发现,它考虑了6种情况。由于左右子节点的情况是对称的,因此只需要讨论当前节点有左子节点的情况。
- (1)如果当前节点是一个左子节点,只需将当前节点的左子节点对父节点的引用改为指向当前节点的父节点,然后将父节点对当前节点的引用改为指向当前节点的左子节点。
- (2)如果当前节点是一个右子节点,只需将当前节点的右子节点对父节点的引用改为指向当前节点的父节点,然后将父节点对当前节点的引用改为指向当前节点的右子节点。
- (3)如果当前节点没有父节点,那它肯定是根节点。调用replaceNodeData方法,替换根节点的key、payload、leftChild和rightChild数据。
代码清单31 情况2:待删除节点只有一个子节点
1 | else: # 只有一个子节点 |
情况3最难处理。如果一个节点有两个子节点,那就不太可能仅靠用其中一个子节点取代它来解决问题。不过,可以搜索整棵树,找到可以替换待删除节点的节点。候选节点要能为左右子树都保持二叉搜索树的关系,也就是树中具有次大键的节点。我们将这个节点称为后继节点,有一种方法能快速找到它。后继节点的子节点必定不会多于一个,所以我们知道如何按照已实现的两种删除方法来移除它。移除后继节点后,只需直接将它放到树中待删除节点的位置上即可。
处理情况3的代码如代码清单32所示。注意,我们用辅助函数findSuccessor和findMin来寻找后继节点,并用spliceOut方法移除它(如代码清单34所示)。之所以用spliceOut方法,是因为它可以直接访问待拼接的节点,并进行正确的修改。虽然也可以递归调用delete,但那样做会浪费时间重复搜索键的节点。
代码清单32 情况3:待删除节点有两个子节点
1 | elif currentNode.hasBothChildren(): # 内部 |
寻找后继节点的代码如代码清单33所示。可以看出,这是TreeNode类的一个方法。它利用的二叉搜索树属性,也是从小到大打印出树节点的中序遍历所利用的。在查找后继节点时,要考虑以下3种情况。
- (1)如果节点有右子节点,那么后继节点就是右子树中最小的节点。
- (2)如果节点没有右子节点,并且其本身是父节点的左子节点,那么后继节点就是父节点。
- (3)如果节点是父节点的右子节点,并且其本身没有右子节点,那么后继节点就是除其本身外父节点的后继节点。
在试图从一棵二叉搜索树中删除节点时,上述第一个条件是唯一重要的。但是,findSuccessor方法还有其他用途,本章末会进行探索。
findMin方法用来查找子树中最小的键。可以确定,在任意二叉搜索树中,最小的键就是最左边的子节点。鉴于此,findMin方法只需沿着子树中每个节点的leftChild引用走,直到遇到一个没有左子节点的节点。代码清单35给出了完整的remove方法。
代码清单33 寻找后继节点
1 | def findSuccessor(self): |
代码清单34 spliceOut方法
1 | def spliceOut(self): |
代码清单35 remove方法
1 | def remove(self, currentNode): |
现在来看看最后一个二叉搜索树接口方法。假设我们想按顺序遍历树中的键。我们在字典中就是这么做的,为什么不在树中试试呢?我们已经知道如何按顺序遍历二叉树——使用中序遍历算法。不过,为了创建迭代器,还需要做更多工作,因为迭代器每次调用只返回一个节点。
Python为创建迭代器提供了一个很强大的函数,即yield。与return类似,yield每次向调用方返回一个值。除此之外,yield还会冻结函数的状态,因此下次调用函数时,会从这次离开之处继续。创建可迭代对象的函数被称作生成器。
二叉搜索树迭代器的代码如代码清单36所示。请仔细看看这份代码。乍看之下,你可能会认为它不是递归的。但是,因为 __iter__ 重载了循环的for x in操作,所以它真的是递归的!由于在TreeNode实例上递归,因此__iter__方法被定义在TreeNode类中。
代码清单 6-36 二叉搜索树迭代器
1 | def __iter__(self): |
搜索树的分析
至此,我们已经完整地实现了二叉搜索树,接下来简单地分析它的各个方法。先分析put方法,限制其性能的因素是二叉树的高度。6.3节曾说过,树的高度是其中节点层数的最大值。高度之所以是限制因素,是因为在搜索合适的插入位置时,每一层最多需要做一次比较。
那么,二叉树的高度是多少呢?答案取决于键的插入方式。如果键的插入顺序是随机的,那么树的高度约为log2n,其中n为树的节点数。这是因为,若键是随机分布的,那么小于和大于根节点的键大约各占一半。二叉树的顶层有1个根节点,第1层有2个节点,第2层有4个节点,依此类推。在完全平衡的二叉树中,节点总数是2h+1-1,其中h代表树的高度。
在完全平衡的二叉树中,左右子树的节点数相同。最坏情况下,put的时间复杂度是O(log2n),其中n是树的节点数。注意,这是上一段所述运算的逆运算。所以,log2n是树的高度,代表put在搜索合适的插入位置时所需的最大比较次数。
不幸的是,按顺序插入键可以构造出一棵高度为n的搜索树!图6-25就是一个例子,这时put方法的时间复杂度为O(n)。
图25 偏斜的二叉搜索树
既然理解了为何说put的性能由树的高度决定,你应该可以猜到,get、in和del也都如此。get在树中查找键,最坏情况就是沿着树一直搜到底也没找到。乍看之下,del可能更复杂,因为在删除节点前可能还得找到后继节点。但是查找后继节点的最坏情况也受限于树的高度,也就是把工作量加一倍。所以,对于不平衡的树来说,最坏情况下的时间复杂度仍是O(n)。
平衡二叉搜索树
在 6.7节中,我们了解了二叉搜索树的构建过程。我们已经知道,当二叉搜索树不平衡时,get 和 put 等操作的性能可能降到 ( ) O n 。本节将介绍一种特殊的二叉搜索树,它能自动维持平衡。这种树叫作 AVL 树,以其发明者 G. M. Adelson-Velskii和 E. M. Landis的姓氏命名。
AVL树实现映射抽象数据类型的方式与普通的二叉搜索树一样,唯一的差别就是性能。实现AVL树时,要记录每个节点的平衡因子。我们通过查看每个节点左右子树的高度来实现这一点。更正式地说,我们将平衡因子定义为左右子树的高度之差。
( ) ( ) balanceFactor height left SubTree height rightSubTree
根据上述定义,如果平衡因子大于零,我们称之为左倾;如果平衡因子小于零,就是右倾;
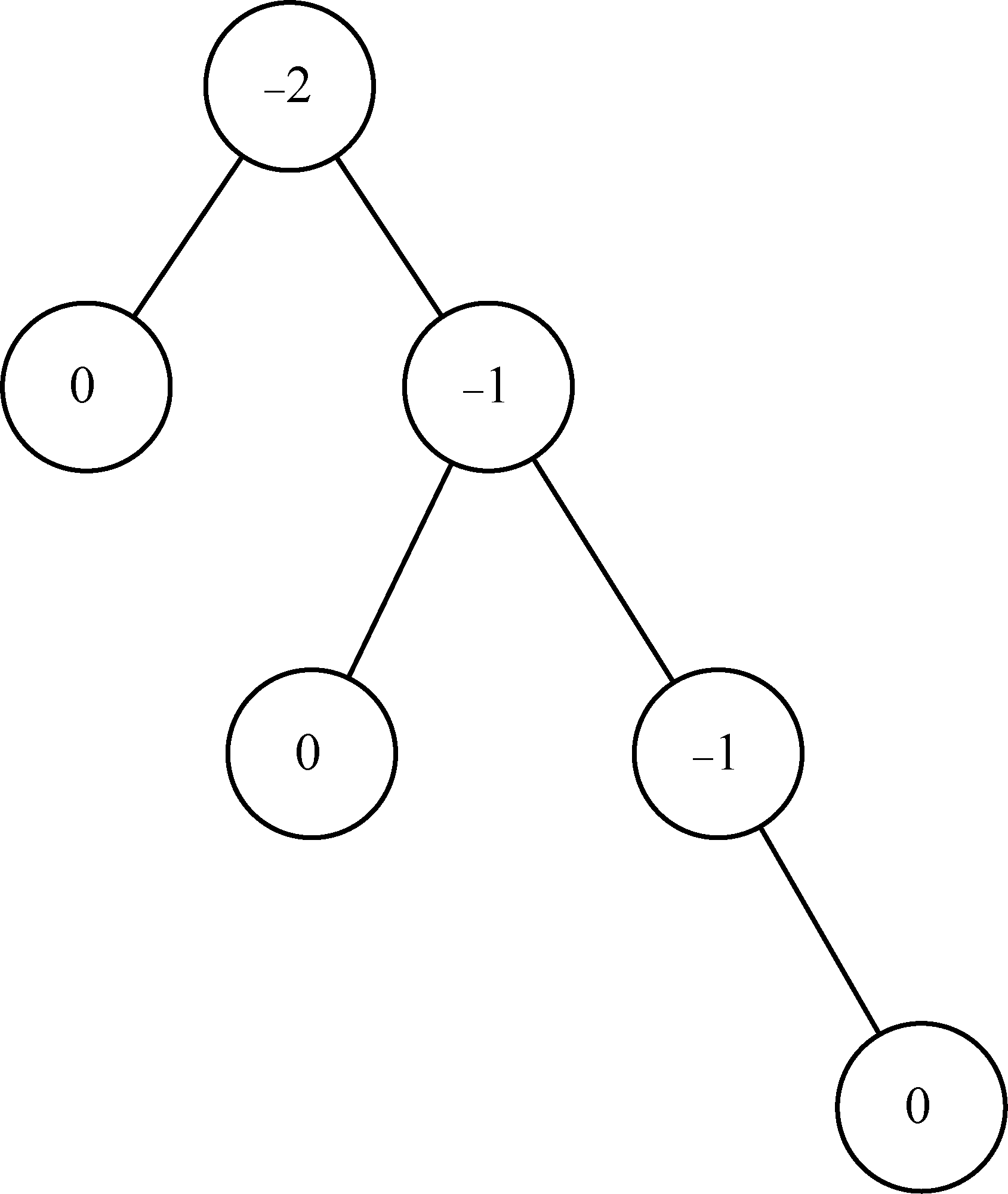
如果平衡因子等于零,那么树就是完全平衡的。为了实现AVL树并利用平衡树的优势,我们将平衡因子为–1、0和 1的树都定义为平衡树。一旦某个节点的平衡因子超出这个范围,我们就需要通过一个过程让树恢复平衡。图26展示了一棵右倾树及其中每个节点的平衡因子。
图26 带平衡因子的右倾树
AVL 树的性能
我们先看看限定平衡因子带来的结果。我们认为,保证树的平衡因子为–1、0或1,可以使关键操作获得更好的大O性能。首先考虑平衡因子如何改善最坏情况。有左倾与右倾这两种可能性。如果考虑高度为0、1、2和 3的树,图27展示了应用新规则后最不平衡的左倾树。
图27 左倾 AVL 树的最坏情况
查看树中的节点数之后可知,高度为 0时有 1个节点,高度为 1时有 2个节点(1 + 1 = 2),高度为 2时有 4个节点(1 + 1 + 2 = 4),高度为 3时有 7个节点(1 + 2 + 4 = 7)。也就是说,当高度为 h时,节点数
h
N 是:
你或许觉得这个公式很眼熟,因为它与斐波那契数列很相似。可以根据它推导出由AVL树的节点数计算高度的公式。在斐波那契数列中,第 i个数是:
一个重要的事实是,随着斐波那契数列的增长,
F F 逐渐逼近黄金分割比例 ,
= 。如果你好奇这个等式的推导过程,可以找一本数学书看看。我们在此直接使用这个
等式,将
i
F 近似为 / 5
i
i
F 。由此,可以将
h
N 的等式重写为:
N h = F h+2 1, h≥1
用黄金分割近似替换,得到:
移项,两边以 2为底取对数,求 h,得到:
在任何时间,AVL树的高度都等于节点数取对数再乘以一个常数(1.44)。对于搜索AVL树来说,这是一件好事,因为时间复杂度被限制为 (log ) O N 。
AVL 树的实现
我们已经证明,保持 AVL 树的平衡会带来很大的性能优势,现在看看如何往树中插入一个键。所有新键都是以叶子节点插入的,因为新叶子节点的平衡因子是零,所以新插节点没有什么限制条件。但插入新节点后,必须更新父节点的平衡因子。新的叶子节点对其父节点平衡因子的影响取决于它是左子节点还是右子节点。如果是右子节点,父节点的平衡因子减一。如果是左子节点,则父节点的平衡因子加一。这个关系可以递归地应用到每个祖先,直到根节点。既然更新平衡因子是递归过程,就来检查以下两种基本情况:
递归调用抵达根节点;
父节点的平衡因子调整为零;
可以确信,如果子树的平衡因子为零,那么祖先节点的平衡因子将不会有变化。
我们将 AVL 树实现为 BinarySearchTree 的子类。首先重载_put方法,然后新写updateBalance辅助方法,如代码清单 6-37 所示。可以看到,除了在第 8 行和第 15 行调用updateBalance 以外, _put 方法的定义和代码清单 6-25中的几乎一模一样。
代码清单 6-37 更新平衡因子
1 | def _put(self, key, val, currentNode): |
新方法updateBalance做了大部分工作,它实现了前面描述的递归过程。updateBalance方法先检查当前节点是否需要再平衡(第 18行)。如果符合判断条件,就进行再平衡,不需要更新父节点;如果当前节点不需要再平衡,就调整父节点的平衡因子。如果父节点的平衡因子非零,那么沿着树往根节点的方向递归调用updateBalance 方法。
如果需要进行再平衡,该怎么做呢?高效的再平衡是让AVL树发挥作用同时不损性能的关键。为了让AVL树恢复平衡,需要在树上进行一次或多次旋转。
要理解什么是旋转,来看一个简单的例子。考虑图6-28中左边的树。这棵树失衡了,平衡因子是–2。要让它恢复平衡,我们围绕以节点 A为根节点的子树做一次左旋。
图28 通过左旋让失衡的树恢复平衡
本质上,左旋包括以下步骤。
- 将右子节点(节点 B)提升为子树的根节点。
- 将旧根节点(节点 A)作为新根节点的左子节点。
- 如果新根节点(节点B)已经有一个左子节点,将其作为新左子节点(节点A)的右子节点。注意,因为节点 B之前是节点 A的右子节点,所以此时节点 A必然没有右子节点。
因此,可以为它添加新的右子节点,而无须过多考虑。
左旋过程在概念上很简单,但代码细节有点复杂,因为需要将节点挪来挪去,以保证二叉搜索树的性质。另外,还要保证正确地更新父指针。
我们来看一棵稍微复杂一点的树,并理解右旋过程。图29 左边的是一棵左倾的树,根节点的平衡因子是 2。右旋步骤如下。
- 将左子节点(节点 C)提升为子树的根节点。
- 将旧根节点(节点 E)作为新根节点的右子节点。
如果新根节点(节点 C)已经有一个右子节点(节点 D),将其作为新右子节点(节点 E)
的左子节点。注意,因为节点 C 之前是节点 E 的左子节点,所以此时节点 E 必然没有左
子节点。因此,可以为它添加新的左子节点,而无须过多考虑。
图29通过右旋让失衡的树恢复平衡了解旋转的基本原理之后,来看看代码。代码清单38给出了左旋的代码。第2行创建一个临时变量,用于记录子树的新根节点。如前所述,新根节点是旧根节点的右子节点。既然临时
变量存储了指向右子节点的引用,便可以将旧根节点的右子节点替换为新根节点的左子节点。
下一步是调整这两个节点的父指针。如果新根节点有左子节点,那么这个左子节点的新父节点就是旧根节点。将新根节点的父指针指向旧根节点的父节点。如果旧根节点是整棵树的根节点,那么必须将树的根节点设为新根节点;如果不是,则当旧根节点是左子节点时,将左子节点的父指针指向新根节点;当旧根节点是右子节点时,将右子节点的父指针指向新根节点(第 10~13行)。
最后,将旧根节点的父节点设为新根节点。这一系列描述很复杂,所以建议你根据图6-28的例子运行一遍函数。 rotateRight 与 rotateLeft 对称,所以留作练习。
代码清单 6-38 左旋
1 | def rotateLeft(self, rotRoot): |
第16~19行需要特别解释一下。这几行更新了旧根节点和新根节点的平衡因子。由于其他移动操作都是针对整棵子树,因此旋转后其他节点的平衡因子都不受影响。但在没有完整地重新计算新子树高度的情况下,怎么能更新平衡因子呢?下面的推导过程能证明,这些代码是对的。
图30 左旋
图30 展示了左旋结果。B 和 D 是关键节点,A、C、E 是它们的子树。针对根节点为 x 的
子树,将其高度记为
x
h 。由定义可知:
( )
( )
A C
A D
newBal B h h
oldBal B h h
D 的旧高度也可以定义为 1 max( , )
C E
h h ,即 D 的高度等于两棵子树的高度的大值加一。因
为
C
h 与
E
h 不变,所以代入第 2 个等式,得到 ( ) (1 max( , ))
A C E
oldBal B h h h 。然后,将两个等
式相减,并运用代数知识简化 ( ) newBal B 的等式。
( ) ( ) ( (1 max( , )))
( ) ( ) (1 max( , ))
( ) ( ) 1 max( , )
( ) ( ) 1 max( , )
A C A C E
A C A C E
A A C E C
C E C
newBal B oldBal B h h h h h
newBal B oldBal B h h h h h
newBal B oldBal B h h h h h
newBal B oldBal B h h h
下面将 ( ) oldBal B 移到等式右边,并利用性质 max( , ) max( , ) a b c a c b c 得到:
( ) ( ) 1 max( , )
C C E C
newBal B oldBal B h h h h
由于
E C
h h 就等于 ( ) oldBal D ,因此可以利用另一个性质 max( , ) min( , ) a b a b 。最后几
步推导如下:
( ) ( ) 1 max(0, ( ))
( ) ( ) 1 min(0, ( ))
newBal B oldbal B oldBal D
newBal B oldBal B oldBal D
至此,我们已经做好所有准备了。如果还记得B是rotRoot而D是newRoot,那么就能看到以上等式对应于代码清单6-38中的第16行:
1 | rotRoot.balanceFactor = rotRoot.balanceFactor + 1 \ |
通过类似的推导,可以得到节点D的等式,以及右旋后的平衡因子。这个推导过程留作练习。
现在你可能认为大功告成了。我们已经知道如何左旋和右旋,也知道应该在什么时候旋转,但请看看图31。节点A的平衡因子为–2,应该做一次左旋。但是,围绕节点A左旋后会怎样呢?
图31 更难平衡的树
左旋后得到另一棵失衡的树,如图32所示。如果在此基础上做一次右旋,就回到了图31的状态。
图32 左旋后,树朝另一个方向失衡
要解决这种问题,必须遵循以下规则。
- 如果子树需要左旋,首先检查右子树的平衡因子。如果右子树左倾,就对右子树做一次右旋,再围绕原节点做一次左旋。
- 如果子树需要右旋,首先检查左子树的平衡因子。如果左子树右倾,就对左子树做一次左旋,再围绕原节点做一次右旋。
图33展示了如何通过以上规则解决图31和图32中的困境。围绕节点C做一次右旋,再围绕节点A做一次左旋,就能让子树恢复平衡。
图33 先右旋,再左旋
rebalance方法实现了上述规则,如代码清单6-39所示。第2行的if语句实现了规则1,第8行的elif语句实现了规则2。
在6.11节中,你将尝试通过先左旋再右旋的方式恢复一棵树的平衡,还会试着为一些更复杂的树恢复平衡。
代码清单6-39 实现再平衡
1 | def rebalance(self, node): |
通过维持树的平衡,可以保证get方法的时间复杂度为$O(\log_2n)$。但这会给put操作的性能带来多大影响呢?我们来看看put操作。因为新节点作为叶子节点插入,所以更新所有父节点的平衡因子最多需要$\log_2n$次操作——每一层一次。如果树失衡了,恢复平衡最多需要旋转两次。每次旋转的时间复杂度是$O(1)$,所以put操作的时间复杂度仍然是$O(\log_2n)$。
至此,我们已经实现了一棵可用的AVL树,不过还没有实现删除节点的功能。我们将删除节点及后续的更新和再平衡的实现留作练习。
映射实现总结
本章和第5章介绍了可以用来实现映射这一抽象数据类型的多种数据结构,包括有序列表、散列表、二叉搜索树以及AVL树。表6-1总结了每个数据结构的性能。
表6-1 映射的不同实现间的性能对比
| put | $O(n)$ | $O(1)$ | $O(n)$ | $O(\log_2n)$ |
| get | $O(\log_2n)$ | $O(1)$ | $O(n)$ | $O(\log_2n)$ |
| in | $O(\log_2n)$ | $O(1)$ | $O(n)$ | $O(\log_2n)$ |
| del | $O(n)$ | $O(1)$ | $O(n)$ | $O(\log_2n)$ |
小结
本章介绍了树这一数据结构。有了树,我们可以写出很多有趣的算法。我们用树做了以下这
些事。
- 用二叉树解析并计算表达式。
- 用二叉树实现映射。
- 用平衡二叉树(AVL树)实现映射。
- 用二叉树实现最小堆。
- 用最小堆实现优先级队列。
关键术语
AVL树 边 层数 堆的有序性
二叉堆 二叉树 二叉搜索树 父节点
高度 根节点 后继节点 后序遍历
节点 路径 前序遍历 树
完全二叉树 兄弟节点 旋转 叶子节点
映射 优先级队列 中序遍历 子节点
子树 最小堆/最大堆
讨论题
1.画出下列函数调用后的树结构。1
2
3
4
5
6
7
8
9
10
11
12>>> r = BinaryTree(3)
>>> insertLeft(r, 4)
[3, [4, [], []], []]
>>> insertLeft(r, 5)
[3, [5, [4, [], []], []], []]
>>> insertRight(r, 6)
[3, [5, [4, [], []], []], [6, [], []]]
>>> insertRight(r, 7)
[3, [5, [4, [], []], []], [7, [], [6, [], []]]]
>>> setRootVal(r, 9)
>>> insertLeft(r, 11)
[9, [11, [5, [4, [], []], []], []], [7, [], [6, [], []]]]
2.为表达式 (4 * 8) / 6 - 3 创建对应的表达式树。
3.针对整数列表 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] ,给出插入列表中整数得到的二叉搜索树。
4.针对整数列表 [10, 9, 8, 7, 6, 5, 4, 3, 2, 1] ,给出插入列表中整数得到的二叉搜索树。
5.生成一个随机整数列表。给出插入列表中整数得到的二叉堆。
6.将前一道题得到的列表作为 buildHeap 方法的参数,给出得到的二叉堆。以树和列表两种形式展示。
7.画出按次序插入这些键之后的二叉搜索树:68、88、61、89、94、50、4、76、66、82。
8.生成一个随机整数列表。画出插入列表中整数得到的二叉搜索树。
9.针对整数列表 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] ,给出插入列表中整数得到的二叉堆。
10.针对整数列表 [10, 9, 8, 7, 6, 5, 4, 3, 2, 1] ,给出插入列表中整数得到的二叉堆。
11.考虑本章实现二叉树的两种方式。在实现为方法时,为什么必须在调用preorder前检查,而在实现为函数时,可以在调用内部检查?
12.给出构建下面这棵二叉树所需的函数调用。
13.对下面这棵树,实施恢复平衡所需的旋转操作。
14.以图30作为出发点,推导出节点 D在更新后的平衡因子等式。
编程练习
- 1.扩展buildParseTree方法,使其能处理字符间没有空格的数学表达式。
- 2.修改buildParseTree和evaluate,使它们支持逻辑运算符(and、or、not)。注意,not是一元运算符,这会让代码有点复杂。
- 3.使用findSuccessor方法,写一个非递归的二叉搜索树中序遍历方法。
- 4.修改二叉搜索树的实现代码,从而实现线索二叉搜索树。为线索二叉搜索树写一个非递归的中序遍历方法。线索二叉搜索树为其中的每个节点都维护着指向后继节点的引用。
- 5.修改二叉搜索树的实现代码,以正确处理重复的键。也就是说,如果键已在树中,就替换有效载荷,而不是用同一个键插入一个新节点。
- 6.创建限定大小的二叉堆。也就是说,堆只保持n个最重要的元素。如果堆的大小超过了n,就会舍弃最不重要的元素。
- 7.整理printexp函数,去掉数字周围多余的括号。
- 8.使用buildHeap方法,针对列表写一个时间复杂度为$O(n\log n)$的排序函数。
- 9.写一个函数,以数学表达式解析树为参数,计算各变量的导数。
- 10.将二叉堆实现为最大堆。
- 11.使用BinaryHeap类,实现一个叫作PriorityQueue的新类。为PriorityQueue类实现构造方法,以及enqueue方法和dequeue方法。
- 12.实现AVL树的delete方法。