思考并回答以下问题:
- 为什么大多数编程语言都使用快速排序?
- 快速排序依赖于一个名为分区的概念。怎么理解?
本章涵盖:
- 分区
- 快速排序
- 快速排序的效率
- 最坏情况
- 快速选择
递归给我们带来了新的算法实现方式,例如上一章的文件系统遍历。本章我们还会看到,递归能使算法效率大大提高。
前几章我们学会了一些排序算法,包括冒泡排序、选择排序和插入排序。但在现实中,数组排序不是通过它们来做的。为了免去大家重复编写排序算法的烦恼,大多数编程语言都自带用于数组排序的函数,其中很多采用的都是快速排序。
虽然它已经实现好了,但我们还是想研究一下它的原理,因为其运用递归来给算法提速的做法极具推广意义。
快速排序真的很快。尽管在最坏情况(数组逆序)下它跟插入排序、选择排序的效率差不多,但在日常多见的平均情况中,它的确表现优异。
快速排序依赖于一个名为分区的概念,所以我们先从它开始了解。
分区
此处的分区指的是从数组随机选取一个值,以其为轴,将比它小的值放到它左边,比它大的值放到它右边。分区的算法实现起来很简单,例子如下所示。
假设有一个下面这样的数组。

从技术上来说,选任意值为轴都可以,我们就以数组最右的值为轴吧。现在轴就是3了,我们把它圈起来。

然后放置指针,它们应该分别指向排除轴元素的数组最左和最右的元素。
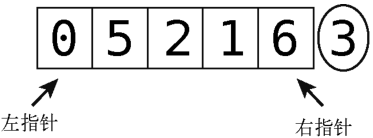
接着就可以分区了,步骤如下。
- (1)左指针逐个格子向右移动,当遇到大于或等于轴的值时,就停下来。
- (2)右指针逐个格子向左移动,当遇到小于或等于轴的值时,就停下来。
- (3)将两指针所指的值交换位置。
- (4)重复上述步骤,直至两指针重合,或左指针移到右指针的右边。
- (5)将轴与左指针所指的值交换位置。
当分区完成时,在轴左侧的那些值肯定比轴要小,在轴右侧的那些值肯定比轴要大。因此,轴的位置也就确定了,虽然其他值的位置还没有完全确定。
让我们来把此流程套到示例数组上。
第1步:拿左指针(正指向0)与轴(值为3)比较。
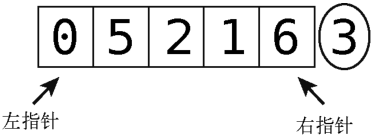
由于0比轴小,左指针可以右移。
第2步:右移左指针。
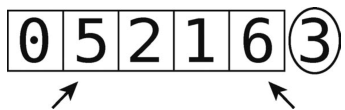
将左指针(值为5)与轴比较。它比轴小吗?不。于是左指针停在这里,下一步我们启动右指针。
第3步:比较右指针(值为6)和轴。它比轴大吗?对。于是右指针左移。
第4步:左移右指针。
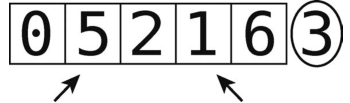
比较右指针(值为1)和轴。它比轴大吗?不。于是右指针停下。
第5步:因为两个指针都停住了,所以交换它们的值。
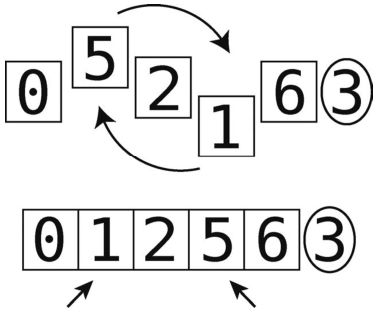
随后,再次启动左指针。
第6步:右移左指针。
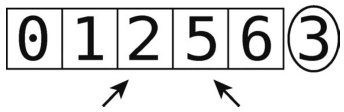
比较左指针(值为2)和轴。它比轴小吗?对。于是继续右移。
第7步:左指针移到下一格子。注意,这时两个指针都指向同一个值了。
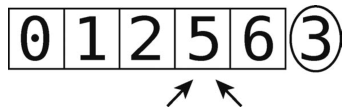
比较左指针和轴。由于左指针的值比轴要大,我们将其停在那里。而且现在左指针与右指针重合,无须再移动指针了。
第8步:到了分区的最后一步,将左指针的值与轴交换位置。
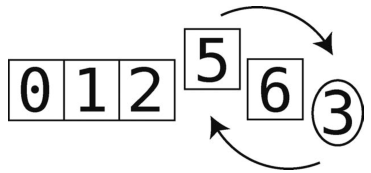
虽然数组还没完全排好序,但我们已完成了一次分区。即比轴(值为3)小的值都聚在了它的左侧,比轴大的值都聚在了它的右侧,这就意味着3已经被放置到正确的位置上了。

下面是用Ruby写的SortableArray类,其中的partition!方法能如上所述对数组进行分区。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43class SortableArray
attr_reader :array
def initialize(array)
@array = array
end
def partition!(left_pointer, right_pointer)
# 总是取最右的值作为轴
pivot_position = right_pointer
pivot = @array[pivot_position]
# 将右指针指向轴左边的一格
right_pointer -= 1
while true do
while @array[left_pointer] < pivot do
left_pointer += 1
end
while @array[right_pointer] > pivot do
right_pointer -= 1
end
if left_pointer >= right_pointer
break
else
swap(left_pointer, right_pointer)
end
end
# 最后将左指针的值与轴交换
swap(left_pointer, pivot_position)
# 根据快速排序的需要,返回左指针
# 具体原因接下来会解释
return left_pointer
end
def swap(pointer_1, pointer_2)
temp_value = @array[pointer_1]
@array[pointer_1] = @array[pointer_2]
@array[pointer_2] = temp_value
end
end
此partition!方法接受两个参数作为左指针和右指针的起始位置,并在结束时返回左指针的最终位置。这是实现快速排序所必需的,下面我们将会看到。
快速排序
快速排序严重依赖于分区。它的运作方式如下所示。
- (1)把数组分区。使轴到正确的位置上去。
- (2)对轴左右的两个子数组递归地重复第1、2步,也就是说,两个子数组都各自分区,并形成各自的轴以及由轴分隔的更小的子数组。然后也对这些子数组分区,以此类推。
- (3)当分出的子数组长度为0或1时,即达到基准情形,无须进一步操作。
将以下quicksort!方法加到刚才的SortableArray类中,快速排序就完整了。1
2
3
4
5
6
7
8
9
10
11
12
13def quicksort!(left_index, right_index)
# 基准情形:分出的子数组长度为 0 或 1
if right_index - left_index <= 0
return
end
# 将数组分成两部分,并返回分隔所用的轴的索引
pivot_position = partition!(left_index, right_index)
# 对轴左侧的部分递归调用 quicksort
quicksort!(left_index, pivot_position - 1)
# 对轴右侧的部分递归调用 quicksort
quicksort!(pivot_position + 1, right_index)
end
想看实际效果的话,可执行以下代码。1
2
3
4array = [0, 5, 2, 1, 6, 3]
sortable_array = SortableArray.new(array)
sortable_array.quicksort!(0, array.length - 1)
p sortable_array.array
再回到刚才的例子。最初的数组是[0, 5, 2, 1, 6, 3],然后我们做了一次分区。所以我们的快速排序已经有一点进度了,目前状态如下。

正如你看到的,其中3为轴。它已经处于正确的位置,接下来对其左右两侧的元素进行排序。
注意,虽然我们看到左侧的元素碰巧已经按顺序排好了,但计算机是不知道的。
下一步,我们把轴左侧的那些元素当作一个独立的数组来分区。
除此之外的元素则先不用看,暂时给它们涂上阴影。
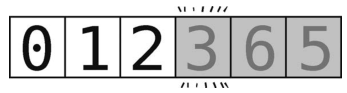
现在,对于这个 [0, 1, 2]的子数组,我们选取其最右端的元素作为轴。于是,轴为 2。
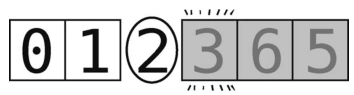
然后,设置左右指针。
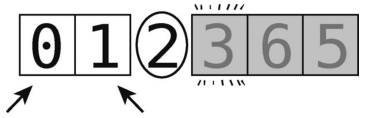
让我们接着之前的第 8步,开始子数组的分区。
第9步:比较左指针(值为0)与轴(值为2)。由于0小于轴,可将左指针右移。
第10步:将左指针右移一格,这时它刚好跟右指针重合了。
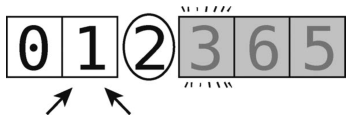
比较左指针与轴。由于 1小于轴,继续右移。
第11步:将左指针右移一格,它便指向轴了。
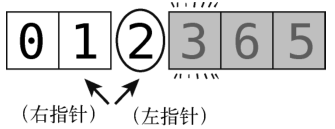
这时左指针的值与轴相等了(因为它正指向轴),左指针停下。
第12步:启动右指针。然而,右指针(值为 1)小于轴,所以不用动。
因为左指针已经跑到右指针的右边了,所以本次分区无须再移动指针。
第13步:最后,将左指针的值跟轴交换。但左指针已经指向轴,因此轴与自身交换,结果没有任何改变。至此,分区完成,轴(值为 2)也到达正确位置了。

于是轴(值为 2)分出了左侧的子数组[0, 1],右侧没有子数组。那么接下来将左侧的[0, 1]分区。
为了专注于 [0, 1] ,我们将其余的元素涂上阴影。
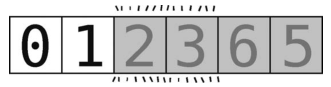
然后选取其最右的元素(值为 1)作为轴。但是左右指针应该如何放置呢?是的,左指针指向0,右指针因为总是从轴左侧那格开始,所以也是指向0,如下所示。
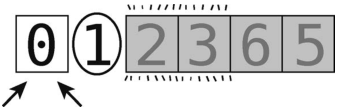
可以开始分区了。
第14步:比较左指针(值为 0)与轴(值为 1)。
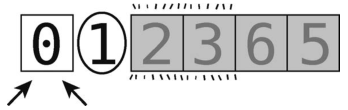
它比轴小,继续右移。
第15步:将左指针往右移一格,这时它指向了轴。

由于左指针不再小于轴了(因为它的值就是轴),于是停下。
第16步:比较右指针与轴。由于其值小于轴,就不用再左移了。而且现在左指针走到了右指针的右边,所以指针无须继续移动,可以进入最后一步。
第17步:将左指针与轴交换。但同样地,这次左指针也指向了轴,所以交换不会产生什么位置改变。于是轴的位置便排好了,分区结束。
此时数组如下所示。
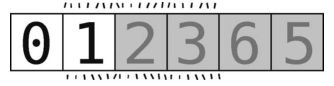
接着,对最近一次的轴的左侧子数组 [0] 进行分区。因为它只包含一个元素,到达了“数组长度为0或1”的基准情形,所以我们什么都不用干。该元素已随着之前的分区被挪到了正确的位置。现在数组如下所示。
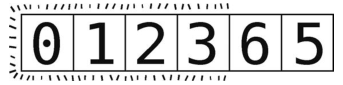
最开始我们以3为轴,然后把其左侧的子数组[0, 1, 2]做了分区。按照约定,现在轮到了它右侧的[6, 5] 。
[0, 1, 2, 3]已经排好了,所以将它们涂上阴影,以便我们专注于[6, 5] 。
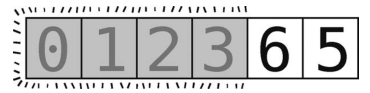
接下来的分区以最右端的元素(值为5)为轴,如下所示。
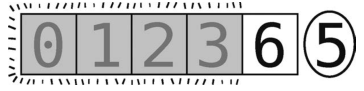
左右指针只能同时指向6。
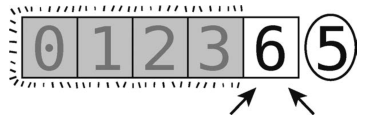
第18步:比较左指针(值为6)与轴(值为5)。由于6大于轴,左指针不再右移。
第19步:本来指着6的右指针应该左移,但6的左边已经没有其他元素了,所以右指针停止。由于左指针与右指针重合,也不用再做任何移动了,可以跳到最后一步。
第20步:将左指针的值与轴交换。
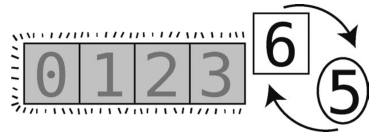
这样轴(值为5)就放到正确位置上了,数组变成了下面这样。
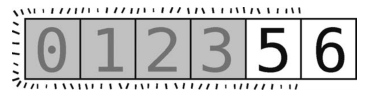
尽管随后我们应该递归地对[5, 6]左右两侧的子数组进行分区,但现在轴左侧没有元素,右侧也只有长度为1的子数组,即到达了基准情形--6已自动挪到了正确位置。

于是整个排序完成!
快速排序的效率
为了搞清楚快速排序的效率,我们先从分区开始。分解来看,你会发现它包含两种步骤。
- 比较:每个值都要与轴做比较。
- 交换:在适当时候将左右指针所指的两个值交换位置。
一次分区至少有N次比较,即数组的每个值都要与轴做比较。因为每次分区时,左右指针都会从两端开始靠近,直到相遇。
交换的次数则取决于数据的排列情况。一次分区里,交换最少会有1次,最多会有N/2次,因为即使所有元素都需要交换,我们也只是将左半部分与右半部分进行交换,如下图所示。

对于随机排列的数据,粗略来算就是N/2的一半,即N/4次交换。于是,N次比较加上N/4次交换,共1.25N步。最后根据大O记法的规则,忽略常数项,得出分区操作的时间为O(N)。
这就是一次分区的效率。但完整的快速排序需要对多个数组以及不同大小的子数组分区,想知道整个过程所花的时间,还要再进一步分析才行。
为了更形象地描述,我们将一个含有8个元素的数组的快速排序过程画了出来。它旁边有每一次分区所作用的元素个数。由于元素值并不重要,因此就不显示了。注意,作用范围就是那些白色的格子。
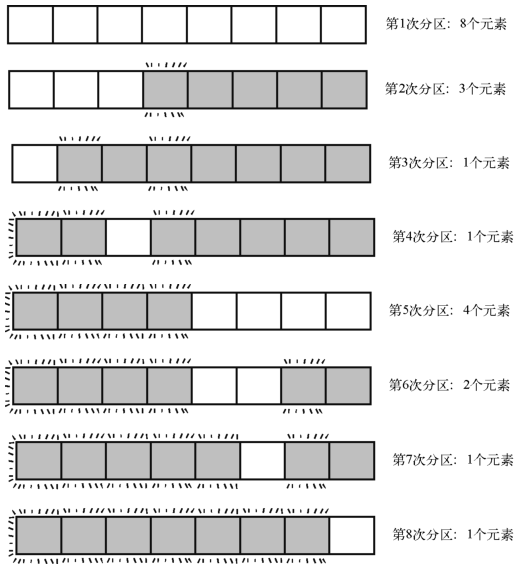
这里有8次分区,但每次作用的范围大小不一。因为只含1个元素的子数组就是基准情形,无须任何交换和比较,所以只有元素量大于或等于2的子数组才要算分区。
由于此例属于平均情况的一种,因此我们假设每次分区大约要花1.25N步,得出:1
2
3
4 8 个元素 * 1.25 = 10 步
3 个元素 * 1.25 = 3.75 步
4 个元素 * 1.25 = 5 步
+ 2 个元素 * 1.25 = 2.5 步
总共约为21步
如果再对不同大小的数组做统计,你会发现N个元素,就要N×log N步。想体会什么是N log N的话,可参考下表。
| 4 | 2 | 8 |
| 8 | 3 | 24 |
| 16 | 4 | 64 |
在上面一个数组含8个元素的例子中,快速排序花了大约21步,也很接近8×log8(等于 24)。这种时间复杂度的算法我们还是第一次遇到,用大O记法来表达的话,它是O(N log N)算法。
快速排序的步数接近N×log N绝非偶然。如果我们以更平均的情况来考察快速排序,就能看出原因了。
快速排序开始时会对整个数组进行分区。假设此次分区会将轴最终安放到数组中央--这也是平均情况--然后我们就要对由此切开的两半进行分区。巧合的是,它们的轴也最终落在各自的中央,分出4个大小为原数组四分之一的子数组。并且,接下来所有分区都出现了这种轴在中央的情况。
这样一来,我们基本上就是在不断地对半切分子数组,直至产生出的子数组长度为1。那么,一个数组要经历多少次分区才能切到这么小呢?如果数组元素有N个,那就是log N次。假设元素有8个,那就要对半切3次,才能分出只有1个元素的子数组。这个原理你应该在二分查找那节学过了。
对两个新的子数组所执行的分区操作,需要处理的数据量还是相当于对原数组所做的分区。如下图所示。
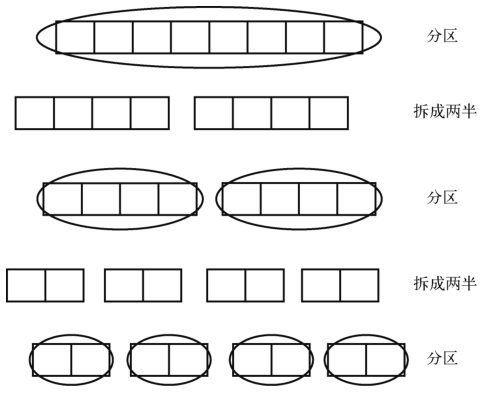
因为等分发生了log N次,而每次都要对总共N个元素做分区,所以总步数为N×log N。
之前我们看到的很多算法,最佳情况都发生在元素有序的时候。但在快速排序里,最佳情况应该是每次分区后轴都刚好落在子数组的中间。
最坏情况
快速排序最坏的情况就是每次分区都使轴落在数组的开头或结尾。导致这种情况的原因有好几种,包括数组已升序排列,或已降序排列。下面我们把这种情况用图来说明一下。
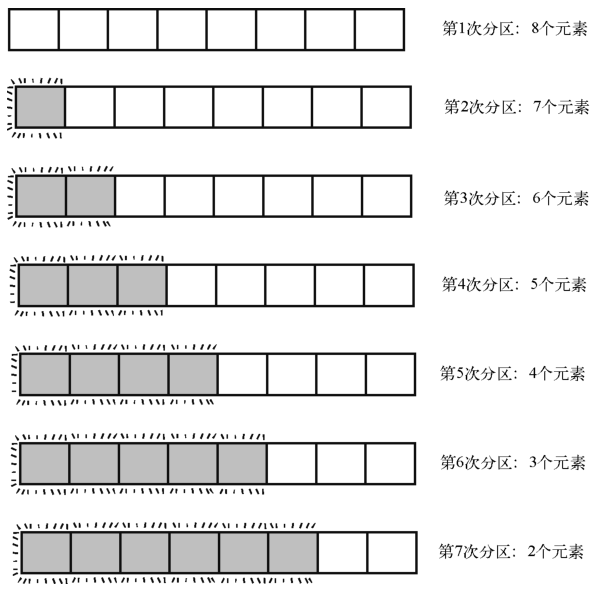
虽然在此情况下,每次分区都只有一次交换,但比较的次数却变得很多。在轴总落在中央的例子里,每次分区都能划分出比原数组小得多的子数组(过程中产生的最大的子数组长度为4),使各部分都能很快地到达基准情形。然而如果轴落在其中一端,前5次分区就需要处理长度大于4的数组。而且这5次分区里,每次所需的比较次数还是和子数组的元素量一样多。
于是在最坏情况下,对8 + 7 + 6 + 5 + 4 + 3 + 2个元素进行分区,一共35次比较。
写成公式的话,就是N个元素,需要N + (N - 1) + (N - 2) + (N - 3) + … + 2步,即N2/ 2步,如下图所示。

又因为大O忽略常数,所以最终我们会说,快速排序最坏情况下的效率为O(N2)。
既然把快速排序分析完了,我们将它与插入排序比较一下。
| 插入排序 | O(N) | O(N2) | O(N2) |
| 快速排序 | O(N log N) | O(N log N) | O(N2) |
虽然快速排序在最好情况和最坏情况都没能超越插入排序,但在最常遇见的平均情况,前者的O(N log N)比后者的O(N2)好得多,所以总体来说,快速排序优于插入排序。
以下是各种时间复杂度的对比。
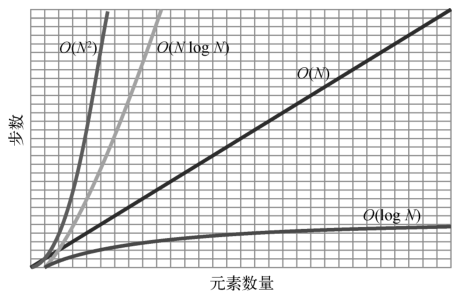
由于快速排序在平均情况下表现优异,于是很多编程语言自带的排序函数都采用它来实现。因此一般你不需要自己写快速排序。但你可能需要学会写快速选择--它是一种类似快速排序的实用算法。
快速选择
假设有一个无序的数组,你不需要将它排序,只要找出里面第10小的值,或第5大的值。就像从一堆测试成绩中找出第25百分位,或找出中等成绩那样。
你首先想到的,可能是把整个数组排序,然后再跳到对应的格子里去找。
但这样做的话,即使是用快速排序那样高效的算法,一般也需要O(N log N)。虽然这也不算差,但一种名为快速选择的算法可以做得更好。快速选择需要对数组分区,这跟快速排序类似,或者你可以把它想象成是快速排序和二分查找的结合。
如之前所述,分区的作用就是把轴排到正确的格子上。快速选择就利用了这一点。
例如要在一个长度为8的数组里,找出第2小的值。
先对整个数组分区。

轴很可能落到数组中间某个地方。

现在轴已安放在正确位置了,因为那是第5个格子,所以我们掌握了数组第5小的值是什么。虽然我们要找的是第2小的值,但刚才的操作足以让我们忽略轴右侧的那些元素,将查找范围缩小到轴左侧的子数组上。这看起来就像是不断地把查找范围缩小一半的二分查找。
然后,继续对轴左侧的子数组分区。
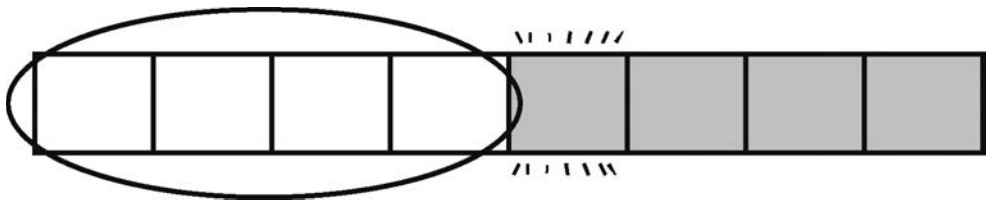
假设子数组的轴最后落到第3个格子上。

现在第3个格子的值已经确定了,该值就是数组第3小的值,第2小的值也就是它左侧的某个元素。于是再对它左侧的元素分区。

这次分区过后,最小和第 2小的元素也就能确定了。
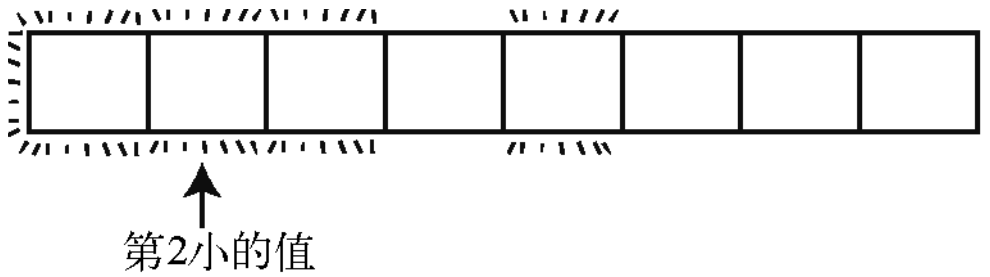
这么一来,我们就可以拿出第2个格子的值,告诉别人找到第2小的元素了。快速选择的优势就在于它不需要把整个数组都排序就可以找到正确位置的值。
如果像快速排序那样,每次分区后还是要处理原数组那么多的数据,就会导致O(N log N)的步数。但快速选择不同,下一次的分区操作只需在上一次分出的一半区域上进行,即值可能存在的那一半。
分析快速选择的效率,你会发现它的平均情况是O(N)。回想每次分区的步数大约等于作用数组的元素量,你便可算出,对于一个含有 8个元素的数组,会有3次分区:第一次处理整个数组的8个元素,第二次处理子数组的4个元素,还有一次处理更小的子数组的2个元素。加起来就是8 + 4 + 2 = 14步。于是8个元素大概是14步。
如果是64个元素,就会是64 + 32 + 16 + 8 + 4 + 2 = 126步;如果是128个元素,就会是254步;如果是256个元素,就会是510步。
用公式来表达,就是对于N个元素,会有N + (N / 2) + (N / 4) + (N / 8) + … + 2步。结果大概是2N步。由于大O忽略常数,我们最终会说快速选择的效率为O(N)。
你可以把以下实现了快速选择的quickselect!方法加到刚才的SortableArray里。你会发现它跟quicksort!很像。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20def quickselect!(kth_lowest_value, left_index, right_index)
# 当子数组只剩一个格子——即达到基准情形时,
# 那我们就找到所需的值了
if right_index - left_index <= 0
return @array[left_index]
end
# 将数组分成两部分,并返回分隔所用的轴的索引
pivot_position = partition!(left_index, right_index)
if kth_lowest_value < pivot_position
quickselect!(kth_lowest_value, left_index, pivot_position - 1)
elsif kth_lowest_value > pivot_position
quickselect!(kth_lowest_value, pivot_position + 1, right_index)
else # 至此 kth_lowest_value 只会等于 pivot_position
# 如果分区后返回的轴的索引等于 kth_lowest_value,
# 那这个轴就是我们要找的值
return @array[pivot_position]
end
end
想要从一个无序数组中找出第2小的值,可以运行如下代码。1
2
3array = [0, 50, 20, 10, 60, 30]
sortable_array = SortableArray.new(array)
p sortable_array.quickselect!(1, 0, array.length - 1)
此方法的第一个参数是查找的位置。因为数组索引从0开始算起,所以我们传入1来查找第2小的值。
总结
由于运用了递归,快速排序和快速选择可以将棘手的问题解决得既巧妙又高效。这也提醒了我们,有些看上去很普通的算法,可能是经过反复推敲的高性能解法。
其实能递归的不只有算法,还有数据结构。后面几章将要接触的链表、二叉树以及图,就利用了自身递归的特性,给我们提供了迅速的数据操作方式。